ЦЕЛЬ РАБОТЫ. Изучить влияние звена чистого запаздывания на устойчивость и динамические характеристики систем автоматического управления (САУ). Приобрести навыки применения критерия Найквиста к исследованию устойчивости систем с запаздыванием.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«СЕВАСТОПОЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

Кафедра «Управление в технических системах»

Отчет

по лабораторной работе №1

ИССЛЕДОВАНИЕ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

С ЗАПАЗДЫВАНИЕМ

Выполнил:

студент группы УТС/б-18-2о

Сусло В.К.

Проверил:

доц. Грушун А.И.

Севастополь 2021

ЦЕЛЬ РАБОТЫ

Изучить влияние звена чистого запаздывания на устойчивость и динамические характеристики систем автоматического управления (САУ). Приобрести навыки применения критерия Найквиста к исследованию устойчивости систем с запаздыванием.

ХОД РАБОТЫ

Вариант 25

1) Построим схему в Simulink

Рисунок 1. Схема в Simulink, отражающая процесс построения графика работы звена чистого запаздывания

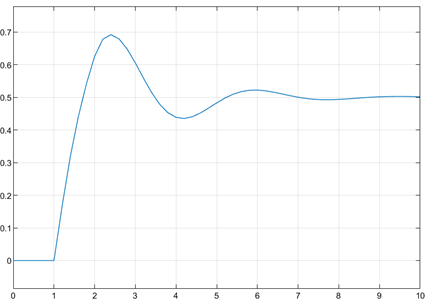
Рисунок 2. График работы Simulink-схемы звена чистого запаздывания

Код:

clc

clear all

a0 = 1; a1 = 7; a2 = 2; a3 = 3

b0 = 4; b1 = 1

sys = tf([1 4],[1 2 7 1])

sys.inputd = 2

nyquist(sys)

hold on

sys =

s + 4

exp(-2*s) * ---------------------

s^3 + 2 s^2 + 7 s + 1

Continuous-time transfer function.

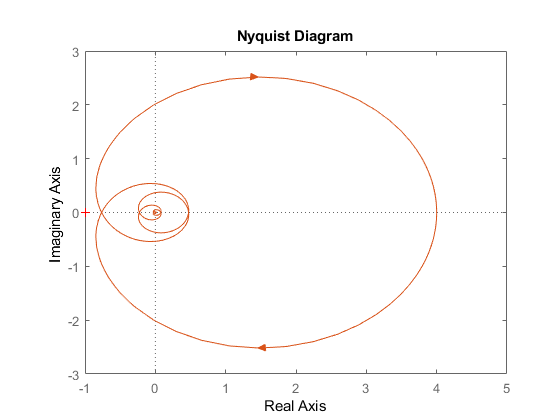
Рисунок 3. Полученный годограф Найквиста, для значений ([1 4], [1 2 7 1])

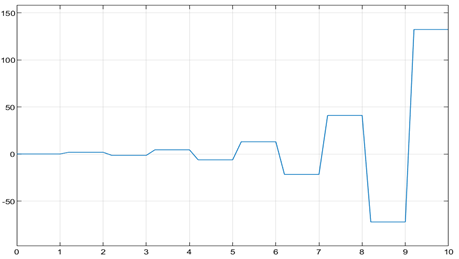
Рисунок 4. Диаграмма работы схемы звена чистого запаздывания, выполненная в программе Proteus Professional.

Рисунок 5. Схема реализации звена чистого запаздывания в программе «Proteus Professional»

ВЫВОД

В ходе выполнения лабораторной работы, было изучено опытным путем влияние звена чистого запаздывания на устойчивость и динамические характеристики САУ.

Из проведенных экспериментов стало ясно ,что САУ является ,сначала, неустойчивой, но, в ходе работы кода, со временем, обретает устойчивое положение .

Это свидетельствует о том, что годограф разомкнутой системы не пересекается с кругом единичного радиуса, а система будет иметь устойчивое положение при любом запаздывании, потому что она не охватывает точку (-1, j0).

Схема, реализованная в программе «Proteus Professional», отражает график, свидетельствующий о возникновении колебаний на протяжении реализации графика звена чистого запаздывания.

В ходе проведения работы, было выяснено, что система является устойчивым звеном чистого запаздывания системы.

Вывод о виде системы был сделан, исходя из описания системы, данной в методических указаниях:

- линейными системами с запаздыванием называются такие САУ, которые, имея в общем ту же самую структуру, что и обыкновенные линейные системы, отличаются от последних тем, что в одном или нескольких из своих звеньев имеют запаздывание во времени начала изменения выходной величины (после начала изменения входной) на величину t, называемую временем чистого запаздывания, причем это время запаздывания остается постоянным и во всем последующем ходе процесса. Иными словами, у звеньев с чистым запаздыванием выходная величина повторяет все изменения входной величины с постоянным сдвигом по времени t, что в свою очередь приводит к сдвигу на t вправо выходной характеристики САУ.