КПрОМА Практикум 2. Упражнение 1.. Упражнение 2.. Упражнение 3.

КПрОМА Практикум 2

Упражнение 1.

Создайте в командном окне матрицы A= 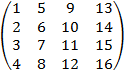, B= и вектор-столбец C= .

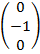а) Одной командой замените две последние строки матрицы A на первые две строки матрицы B.

б) Одной командой замените третий столбец матрицы B столбцом С.

в) Одной командой создайте новую матрицу D размера 7*4, добавив снизу к четырем строкам матрицы A три строки матрицы B.

г) Последние три элемента второй строки матрицы B замените на первые три элемента последней строки матрицы A.

д) Одной командой утройте все элементы второго столбца матрицы D.

Решение:

clc A=[1:4;5:8;9:12;13:16]; A=A' B=[1:4]; B=[B;B;B] C=[0;-1;0] D1=[A(1:2,:);B(1:2,:)]%ex 1 а) D2=[B(:,1:2) C B(:,4)]%ex 1 б) D=[A; B]%ex 1 в) D4=[B(1,:); B(2,1) A(4,2:4); B(3,:)]%ex 1 г) D5=[D(:,1) D(:,2).*3 D(:,3:4)]%ex 1 д)

A = 1 5 9 13 2 6 10 14 3 7 11 15 4 8 12 16 B = 1 2 3 4 1 2 3 4 1 2 3 4 C = 0 -1 0 D1 = 1 5 9 13 2 6 10 14 1 2 3 4 1 2 3 4 D2 = 1 2 0 4 1 2 -1 4 1 2 0 4 D = 1 5 9 13 2 6 10 14 3 7 11 15 4 8 12 16 1 2 3 4 1 2 3 4 1 2 3 4 D4 = 1 2 3 4 1 8 12 16 1 2 3 4 D5 = 1 15 9 13 2 18 10 14 3 21 11 15 4 24 12 16 1 6 3 4 1 6 3 4 1 6 3 4

Упражнение 2.

Создайте в командном окне матрицы A= 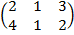, B= и C=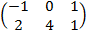

а) Укажите пары матриц, которые можно поэлементно сложить, вычесть, умножить. Проделайте в командном окне соответствующие действия.

б) Укажите пары матриц, которые можно сложить, вычесть, перемножить в

соответствии с правилами линейной алгебры. Проделайте в командном окне

соответствующие действия.

Решение:

%ex2 A=[2 1 3;4 1 2];B=[1:4]; B=[B;B;B]; C=[-1 0 1;2 4 1]; S=A+C S1=A-C S2=A.*C M1=A*B M2=C*B format short E=[2:0.5:11.5]

S = 1 1 4 6 5 3 S1 = 3 1 2 2 -3 1 S2 = -2 0 3 8 4 2 M1 = 6 12 18 24 7 14 21 28 M2 = 0 0 0 0 7 14 21 28 E = Columns 1 through 5 2.0000 2.5000 3.0000 3.5000 4.0000 Columns 6 through 10 4.5000 5.0000 5.5000 6.0000 6.5000 Columns 11 through 15 7.0000 7.5000 8.0000 8.5000 9.0000 Columns 16 through 20 9.5000 10.0000 10.5000 11.0000 11.5000

Упражнение 3.

а) Создать вектор-строку значений переменной x с 20 элементами, у которой первый элемент равен 2, а каждый следующий больше предыдущего на 0,5.

Вычислить значения функции 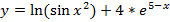при каждом значении x (результат получить в виде вектор-строки).

б) Используя команду linspace, создать вектор-строку с 10 элементами, первый элемент которой равен 2, а последний 4,2.

Вычислить значения функции 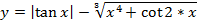при каждом значении x (результат получить в виде вектор-строки).

Решение:

%ex3 a x=[2:0.5:11.5], B=sin(x); C=B.*B; D=log(C); E=4*exp(5-x); y=D+E %ex3 b x=linspace(2,4.2,10), y=abs(tan(x))-(x.^4+cot(x.*2)).^(1/3)

x = Columns 1 through 5 2.0000 2.5000 3.0000 3.5000 4.0000 Columns 6 through 10 4.5000 5.0000 5.5000 6.0000 6.5000 Columns 11 through 15 7.0000 7.5000 8.0000 8.5000 9.0000 Columns 16 through 20 9.5000 10.0000 10.5000 11.0000 11.5000 y = Columns 1 through 5 80.1520 47.7032 25.6399 15.8316 10.3158 Columns 6 through 10 6.5494 3.9161 1.7285 -1.0786 -2.1806 Columns 11 through 15 -0.2988 0.2003 0.1778 -0.3293 -1.6996 Columns 16 through 20 -5.1321 -1.1906 -0.2400 0.0099 -0.2600 x = Columns 1 through 5 2.0000 2.2444 2.4889 2.7333 2.9778 Columns 6 through 10 3.2222 3.4667 3.7111 3.9556 4.2000 y = Columns 1 through 5 -0.3794 -1.6946 -2.6005 -3.3676 -4.0647 Columns 6 through 10 -4.7673 -4.9255 -5.1100 -5.1964 -4.9942

Упражнение 4.

Объем конуса вычисляется по формуле 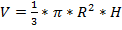, а площадь поверхности по формуле 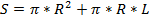, где R - радиус основания, H - высота, L - образующая конуса. Найдите объемы и площади поверхности конусов с радиусом основания

R=5 и высотой H, равной 5, 6,7, …, 14. Выведите на экран результаты в таблице с тремя строками, указав в первой строке значения H, во второй – соответственные значения объем конуса, в третьей -площадь его поверхности. Упражнение выполните с использованием скрипт-файла.

Решение:

%ex4 R=5; H=[5:14]; L=sqrt(R*R+H.*H); V=H.*(1/3)*pi*R*R; S=pi*R*R+L.*pi*R; T=[H; V; S]

T = Columns 1 through 5 5.0000 6.0000 7.0000 8.0000 9.0000 130.8997 157.0796 183.2596 209.4395 235.6194 189.6119 201.2229 213.6648 226.7284 240.2632 Columns 6 through 10 10.0000 11.0000 12.0000 13.0000 14.0000 261.7994 287.9793 314.1593 340.3392 366.5191 254.1602 268.3399 282.7433 297.3264 312.0555

Упражнение 5.

Коэффициент трения µ может быть определён экспериментально измерением силы F, необходимой для перемещения тела массой m. Когда F измерена и m известна, коэффициент трения может быть вычислен по формуле 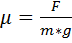(g=9,81 м/с^2 )

Результаты измерения F в 9 испытаниях приведены в таблице ниже. Определите коэффициент трения в каждом испытании и среднее значение при всех испытаниях.

Масса, m (кг)
Сила, F (Н)	12.5	23,5	30,1	60,5	71,2	101,7		180,9

Упражнение выполните с использованием скрипт-файла.

Решение:

%ex5 m=[2 4 5 10 12 17 20 30 50]; F=[12.5 23.5 30.1 60.5 71.2 101.7 117 180.9 293]; g=9.81; Ft=m.*g; k=F./Ft

k = Columns 1 through 5 0.6371 0.5989 0.6137 0.6167 0.6048 Columns 6 through 9 0.6098 0.5963 0.6147 0.5973