Пермский национальный исследовательский политехнический университет»

Министерство науки и высшего образования Российской Федерации

Федеральное государственное автономное образовательное учреждение

высшего образования

«Пермский национальный исследовательский политехнический университет»

Электротехнический факультет

Кафедра «Микропроцессорные средства автоматизации»

Факультет: Электротехнический

Кафедра: «Электромеханика»

Направление: 13.03.02 «Электроэнергетика и электротехника»

Форма обучения: очная

Отчет по лабораторной работе №2

по дисциплине «Теория автоматического управления»

на тему «Исследование устойчивости линейных систем автоматического управления»

Выполнил студент

гр._ЭМ-18-1б
Томилин В.А.

(Фамилия, имя, отчество)

__________________

(подпись)

Проверил:

Канд. техн. наук. Доцент каф. «Микропроцессорные средства автоматизации»

(должность руководителя, кафедра)

Коломыцев Вячеслав Григорьевич

(Ф.И.О. руководителя)

___________ _________________________

(оценка) (подпись)

_____________

(дата)

Пермь 2021

Цель работы

Экспериментальное исследование устойчивости линейных САУ, исследование влияния параметров системы на устойчивость, определение критического передаточного коэффициента разомкнутой системы. Модельно-экспериментальное определение временных и частотных характеристик САУ. Определение запасов устойчивости.

1. Проведите исследование устойчивости системы управления уровнем жидкости в резервуаре различными методами.

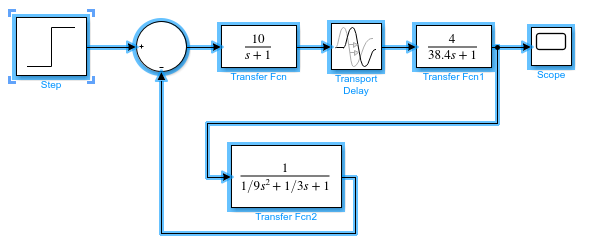
Рисунок 1 – Структурная схема системы управления уровнем жидкости в резервуаре

1.1. Исследуйте выполнение необходимого условия устойчивости Рауса по коэффициентам характеристического полинома замкнутой системы

num1=[10];den1=[1 1];

sys1=tf(num1,den1);

[num2,den2]=pade(1,2);

sys2=tf(num2,den2);

num3=[4];den3=[38.4 1];

sys3=tf(num3,den3);

num4=[1];den4=[1/9 1/3 1];

sys4=tf(num4,den4);

sys5=series(sys1,sys2);

sys6=series(sys5,sys3);

syss=feedback(sys6,sys4,-1);

syssm=minreal(syss)

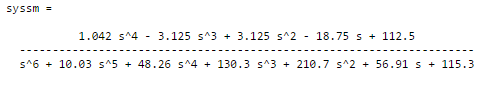
Исходя из необходимого, но недостаточного условия устойчивости Рауса есть положительность коэффициентов характеристического уравнения системы, система условно устойчива.

Передаточная функция разомкнутой системы:

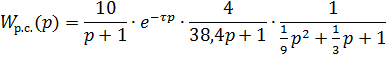
где 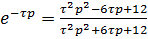, при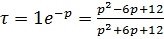

Составим характеристический полином разомкнутой системы:

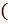p+1)(p²+6p+12)(38,4p+1)(1/9·p²+1/3·p+1)=0

Тогда корни характеристического полинома разомкнутой системы будут следующие:
p₁=-2; p₂=-3+1.73i; p₃=-3-1.73i; p₄=-1/38.4; p₅=-0,6+2,59i; p₆=-0,5-2,59i.

Все корни находятся в левой части комплексной плоскости.

1.2. Определите устойчивость по корням характеристического уравнения замкнутой системы на основе теоремы А.М.Ляпунова

num1=[10];den1=[1 1];

sys1=tf(num1,den1);

[num2,den2]=pade(1,2);

sys2=tf(num2,den2);

num3=[4];den3=[38.4 1];

sys3=tf(num3,den3);

num4=[1];den4=[1/9 1/3 1];

sys4=tf(num4,den4);

sys5=series(sys1,sys2);

sys6=series(sys5,sys3);

syss=feedback(sys6,sys4,-1);

syssm=minreal(syss);

p=pole(syssm)

p =

-3.7261 + 1.9846i

-3.7261 - 1.9846i

-1.3370 + 3.0242i

-1.3370 - 3.0242i

0.0501 + 0.7676i

0.0501 - 0.7676i

Согласно теореме А.М. Ляпунова, когда среди корней (характеристического уравнения) определяющего уравнения находятся такие, вещественные части которых положительные, невозмущенное движение неустойчиво. Таким образом, замкнутая система неустойчива.

1.3. Примените критерий устойчивости Гурвица или Раусадля исследования устойчивости системы, если передаточная функция замкнутой системы известна

m6=[10.02 130.1 56 0 0 0;1 48.22 210.3 115.2 0 0;0 10.02 130.1 56 0 0;0 1 48.22 210.3 115.2 0;0 0 10.02 130.1 56 0;0 0 1 48.262 210.3 115.2]

delta6=det(m6)

m6 =

10.0200 130.1000 56.0000 0 0 0

1.0000 48.2200 210.3000 115.2000 0 0

0 10.0200 130.1000 56.0000 0 0

0 1.0000 48.2200 210.3000 115.2000 0

0 0 10.0200 130.1000 56.0000 0

0 0 1.0000 48.2620 210.3000 115.2000

delta6 =

-1.1077e+10

Согласно критерию Гурвица, необходимо и достаточно, чтобы при положительном коэффициенте характеристического уравнения α₀ главный определитель Гурвица и все его диагональные миноры должны быть положительными. Соответственно, система неустойчива.

1.4. Примените критерий устойчивости Найквиста для АФХ разомкнутой системы

num1=[10];den1=[1 1];

sys1=tf(num1,den1);

[num2,den2]=pade(1,2);

sys2=tf(num2,den2);

num3=[4];den3=[38.4 1];

sys3=tf(num3,den3);

num4=[1];den4=[1/9 1/3 1];

sys4=tf(num4,den4);

sys5=series(sys1,sys2);

sys6=series(sys5,sys3);

sys7=series(sys6,sys4);

nyquist(sys7)

Система неустойчива.

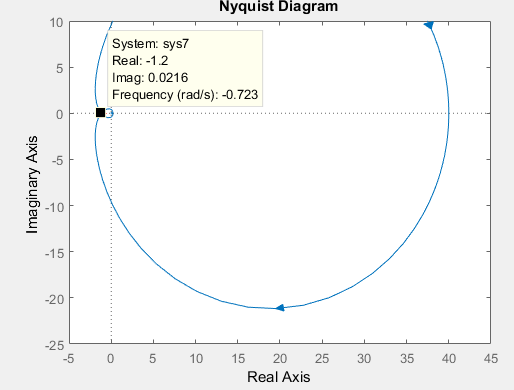
Рисунок 2 – График амплитудно-фазовой характеристики разомкнутой системы

1.5. Примените критерий устойчивости Найквиста для ЛЧХ разомкнутой системы. Если система устойчива, определите запасы устойчивости.

num1=[10];den1=[1 1];

sys1=tf(num1,den1);

[num2,den2]=pade(1,2);

sys2=tf(num2,den2);

num3=[4];den3=[38.4 1];

sys3=tf(num3,den3);

num4=[1];den4=[1/9 1/3 1];

sys4=tf(num4,den4);

sys5=series(sys1,sys2);

sys6=series(sys5,sys3);

sys7=series(sys6,sys4);

sys7m=minreal(sys7);

w=logspace(-1,1,200);

bode(sys7m,w)

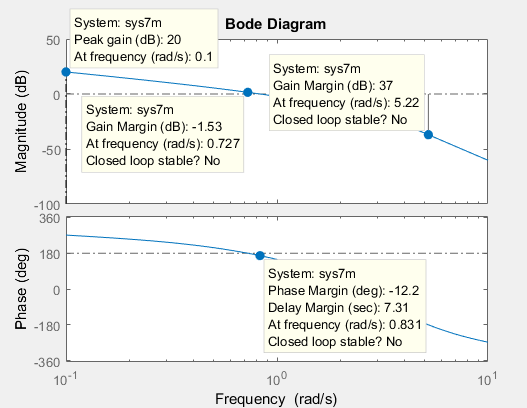
Рисунок 3 – График логарифмической частотной характеристики

Согласно критерию Найквиста, для ЛЧХ, система является условно- устойчивой, так как необходимо и достаточно, чтобы при всех значениях w, где L(w)>0, разность числа положительных и отрицательных переходов фазовой характеристики разомкнутой системы через линии ±(2k+1)p (k=0,1,2,…) равнялась m/2, где m - число полюсов с положительной вещественной частью в передаточной функции разомкнутой цепи системы.

m=0, т.к. все корни имеют отрицательную вещественную часть и находятся в левой части комплексной плоскости, количество переходов фазовой характеристики разомкнутой системы – это минус единица. Из этого следует, что условие устойчивости Найквиста не выполняется и система неустойчива.

1.6. Исследуйте влияние запаздывания τ на устойчивость системы

tau=0.5;

num1=[10];den1=[1 1];

sys1=tf(num1,den1);

[num2,den2]=pade(tau,2);

sys2=tf(num2,den2);

num3=[4];den3=[38.4 1];

sys3=tf(num3,den3);

num4=[1];den4=[1/9 1/3 1];

sys4=tf(num4,den4);

sys5=series(sys1,sys2);

sys6=series(sys5,sys3);

sys7=series(sys6,sys4);

sys7m=minreal(sys7);

w=logspace(-1,1,200);

bode(sys7m,w)

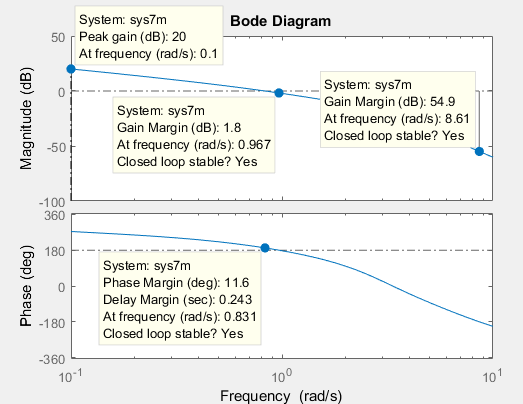
Рисунок 4 – График переходной характеристики системы при τ = 0,5

При τ = 0,5 система устойчива.

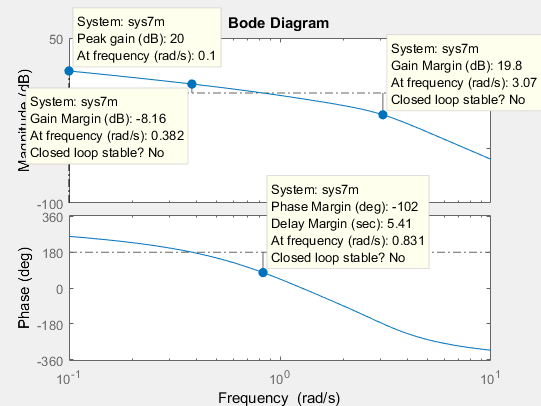
Рисунок 5 – График переходной характеристики системы при τ = 3

При τ = 3 система неустойчива.

1.7. Проведите исследование устойчивости системы по переходным характеристикам в интерактивной среде Simulink

1.7.1.Для случая, когда: Крс = Крскр

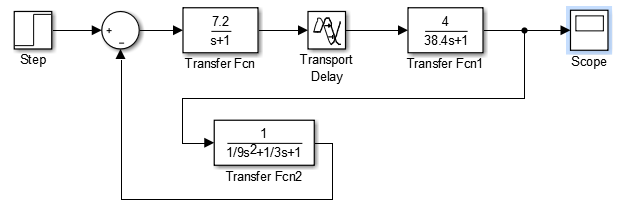
Рисунок 6 – Схема, с условием, что Крс = Крскр

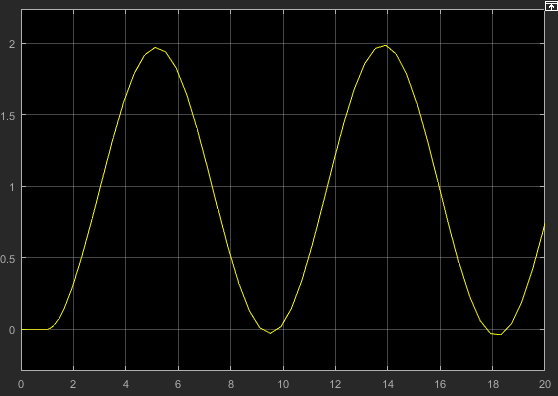
Рисунок 7 – График переходной характеристики для случая, когда: Крс = Крскр, при

1.7.2. Для случая, когда: Крс>КрскрКрс

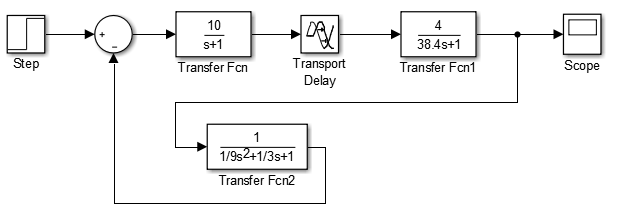
Рисунок 8 – Схема, с условием, что Крс>Крскр

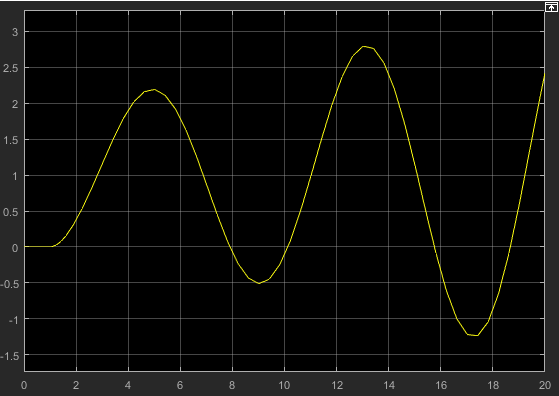
Рисунок 9 – График переходной характеристики для случая, когда: Крс>Крскр

1.7.3.Для случая, когда: Крс<КрскКрс

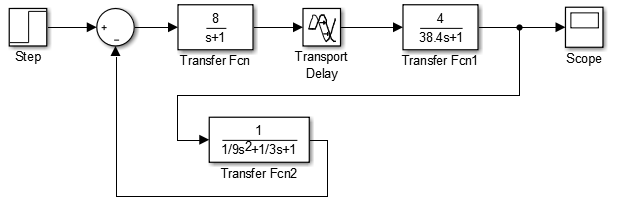
Рисунок 10 – Схема, с условием, что Крс<Крскр

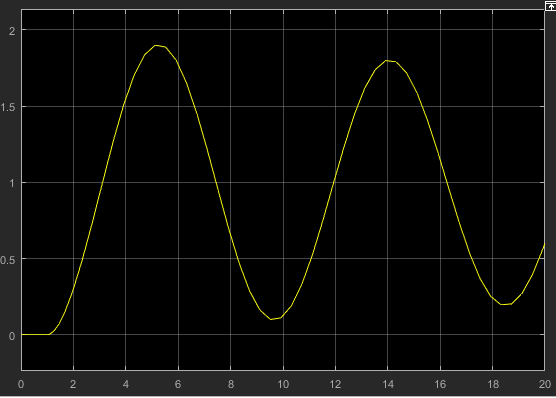
Рисунок 11 – График переходной характеристики для случая, когда: Крс<Крскр

2. Проведите исследование устойчивости системы управления вертикальным взлётом самолёта (аналогичен старт ракеты).

Рисунок 12 – Структурная схема системы управления вертикальным взлётом самолета

Исходя из графика (рисунок 13) переходной характеристики системы управления вертикальным взлётом самолета, можно сделать вывод, что система устойчива.

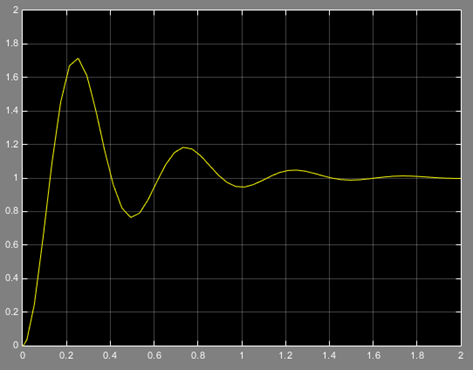
Рисунок 13 – График переходной характеристики системы управления вертикальным взлётом самолета

2.1. Оцените устойчивость системы по условию Рауса

nump=[200 400];

denp=[1 10];

Wp=tf(nump,denp)

numc=[1.28];

denc=[1.28 -1 0];

Wc=tf(numc,denc)

Wsr=Wp*Wc/(1+Wp*Wc)

Wsrm=minreal(Wsr)

Wp =

200 s + 400

-----------

s + 10

Wc =

1.28

-----------

1.28 s^2 - s

Wsr =

327.7 s^4 + 3676 s^3 + 3482 s^2 - 5120 s

----------------------------------------------------------

1.638 s^6 + 30.21 s^5 + 441.3 s^4 + 3440 s^3 + 3582 s^2 - 5120 s

Wsrm =

200 s + 400

-------------------------------

s^3 + 9.219s^2 + 192.2s + 400

Согласно необходимому условию Рауса, необходимым, но недостаточным условием устойчивости САУ, является положительность коэффициентов характеристического уравнения системы. Таким образом, данная система является возможно устойчивой.

2.2.Проведите исследование устойчивости системы по критерию Гурвица

m3=[9.219 400 0;1 192.2 0;0 9.219 400]

delta3=det(m3)

m2=[9.219 400;1 192.2]

delta2=det(m2)

m3 =

9.2189 400.0000 0

1.0000 192.2000 0

0 9.21890 400.0000

delta3 =

5.4875e+05

m2 =

9.2189 400.0000

1.0000 192.2000

delta2 =

1.3718ze+03

Главный определить и все его диагональные миноры положительные, а значит, критерий Гурвица выполняется, и система является устойчивой.

2.3.Проведите исследование устойчивости системы по теоремам А.М. Ляпунова

num=[200 400];

den=[1 9.2189 192.2 400];

Wsr=tf(num,den)

pzmap(Wsr)

Wsr =

200 s + 400

-------------------------------

s^3 + 9.219s^2 + 192.2s + 400

Рисунок 14 – Расположение полюсов и нулей характеристического полинома системы на комплексной плоскости.

Корни характеристического уравнения системы имеют отрицательные вещественные части, нулевых корней нет, а, следовательно, исходя из теоремы А.М. Ляпунова, система устойчива.

2.4. Проведите исследование устойчивости системы по критерию Найквиста для АФХ

nump=[200 400];

denp=[1 10];

Wp=tf(nump,denp)

numc=[1.28];

denc=[1.28 -1 0];

Wc=tf(numc,denc)

Wpc=Wp*Wc

nyquist(Wpc)

Wp =

200 s + 400

-----------

s + 10

Wc =

1.28

-----------

1.28 s^2 - s

Wpc =

256 s + 512

-----------------------

1.28 s^3 + 11.8 s^2 - 10 s

Если система устойчива в разомкнутом состоянии, то для устойчивости замкнутой системы необходимо и достаточно, чтобы при изменении амплитудно-фазовая частотная характеристика (АФЧХ) системы в разомкнутом состоянии не охватывала точку с координатами (-1, j0).

Для устойчивости замкнутой системы, разомкнутая цепь которой неустойчива, требуется, чтобы амплитудно-фазовая характеристика разомкнутой цепи (с дополнением в бесконечности для систем с нулевыми и чисто мнимыми полюсами передаточной функции разомкнутой системы) охватывала точку (-1, j0) против часовой стрелки на угол mp, где m - число полюсов с положительной вещественной частью в передаточной функции неустойчивой разомкнутой цепи системы.

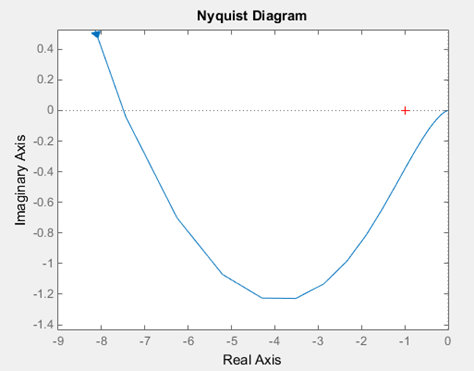
Рисунок 15 – Амплитудно-фазовая характеристика разомкнутой системы.

2.5.Исследование устойчивости системы по критерию Найквиста для ЛЧХ

nump=[200 400];

denp=[1 10];

Wp=tf(nump,denp)

numc=[1.28];

denc=[1.28 -1 0];

Wc=tf(numc,denc)

Wpc=Wp*Wc

margin(Wpc)

Wp =

200 s + 400

-----------

s + 10

Wc =

1.28

-----------

1.28 s^2 - s

Wpc =

256 s + 512

-----------------------

1.28 s^3 + 11.8 s^2 - 10 s

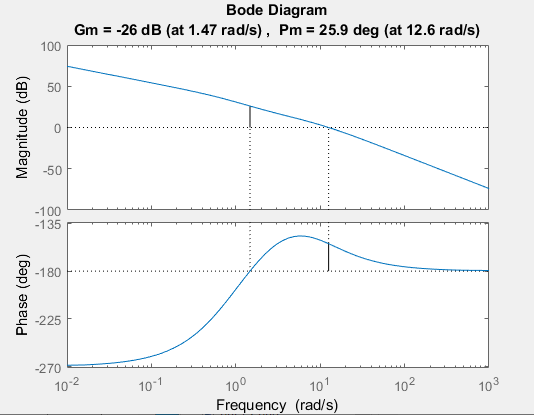
Рисунок 16 – График логарифмической частотной характеристики разомкнутой системы.

Согласно критерию Найквиста, для ЛЧХ, система является устойчивой, так как необходимо и достаточно, чтобы при всех значениях w, где L(w)>0, разность числа положительных и отрицательных переходов фазовой характеристики разомкнутой системы через линии ±(2k+1)p (k=0,1,2,…) равнялась m/2, где m - число полюсов с положительной вещественной частью в передаточной функции разомкнутой цепи системы.

Здесь m=1 , т.к. имеется корень с положительной вещественной частью, есть один положительный переход и один отрицательный полупереход Þ система устойчива.

2.6.Проведите исследование устойчивости системы по переходной характеристике

num=[200 400];

den=[1 9.219 192.2 400];

Wsr=tf(num,den)

step(Wsr)

Wsr =

200 s + 400

-------------------------------

s^3 + 9.219 s^2 + 192.2s + 400

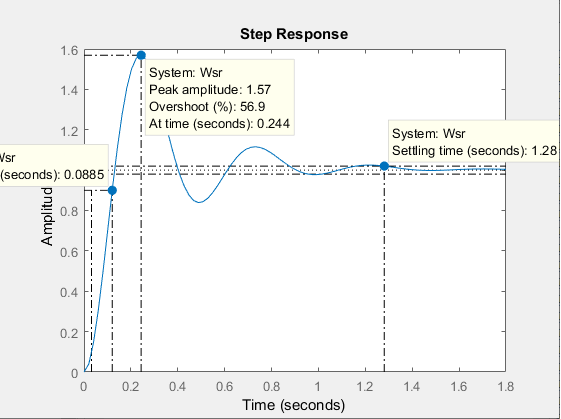
Рисунок 17 – График переходной характеристики.

Исходя из графика переходной характеристики, можно сделать вывод, что система устойчива.

2.7.Проведите исследование устойчивости системы управления вертикальным взлётом самолёта (аналогичен старт ракеты) в Simulink.

2.7.1. Система устойчива:

Рисунок 18 – Схема, с параметрами регулятора подобранными для устойчивой системы.

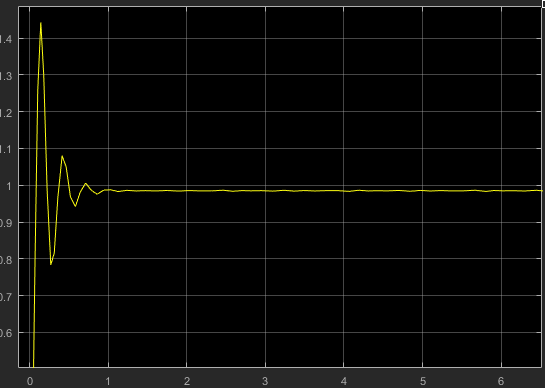
Рисунок 19 – График переходной характеристики устойчивой системы.

2.7.2 Система на границе устойчивости

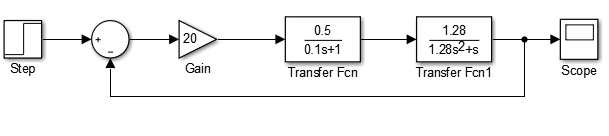
Рисунок 20– Схема, с параметрами регулятора подобранными для системы на границе устойчивости.

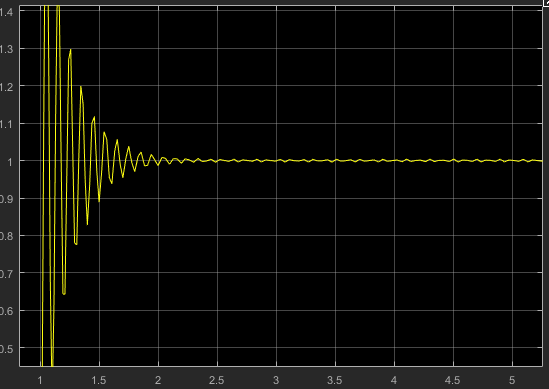
Рисунок 21 – График переходной характеристики системы на границе устойчивости.

2.7.3. Неустойчивая система.

Рисунок 22 – Схема, с параметрами регулятора подобранными для неустойчивой системы.

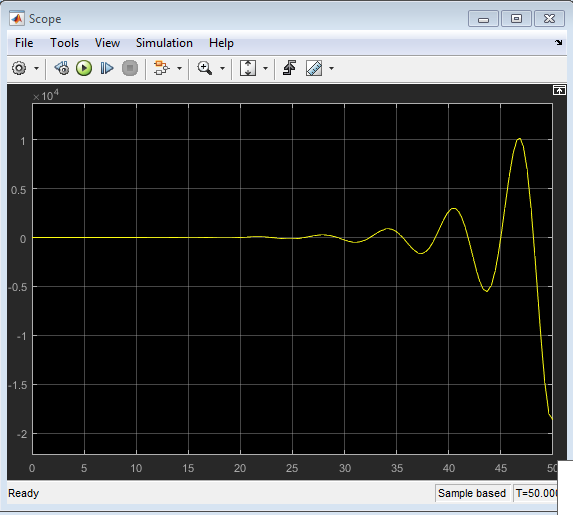
Рисунок 23 – График переходной характеристики неустойчивой системы.

3. Исследуйте устойчивость системы чтения информации с жёсткого диска компьютера в Simulink.

Рисунок 24 – Структурная схема системы управления положением головки дисковода с учётом упругости пластины.

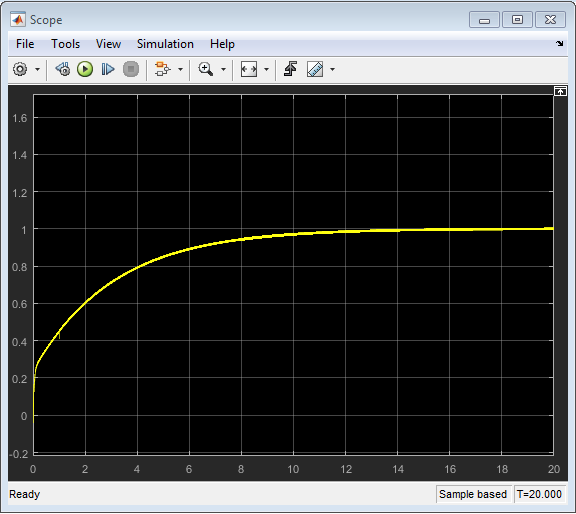
Рисунок 25 – График передаточной функции системы чтения информации с жёсткого диска компьютера.

Исходя из графика передаточной функции системы чтения информации с жёсткого диска компьютера, можно сделать вывод, что система устойчива.

Заключение

Были получены навыки работы с замкнутыми и разомкнутыми схемами, с помощью проведены опытов об установление устойчивости систем САУ экспериментальным путем, а также установлено влияние различных параметров на устойчивость систем, определение критического передаточного коэффициента разомкнутой системы, и, всё это, также путем моделирования схемыопределения их временных и частотных характеристик САУ, сопровождая данные исследования и определением запаса устойчивости рассматриваемых схем.

Вопросы были выданы очно 18.05.21.

Вопросы:

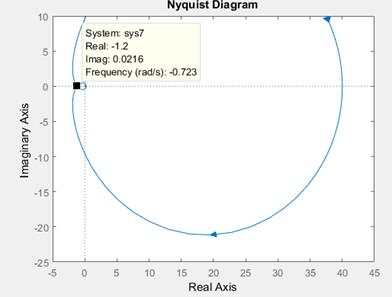
1. Критерий Найквиста для АФХ (рис.2).

1. Размыкаем структурную схему исследуемой системы у входа обратной связи в узел сравнения сигналов.

2. Записываем передаточную функцию разомкнутой системы, считая входом выход сигнала из суммирующего узла, а выходом вход обратной связи в суммирующий узел (находим передаточную функцию разомкнутой системы, как произведение передаточных функций всего контура).

3. Определяем численные значения полюсов (корней знаменателя) передаточной функции разомкнутой системы.

4. Располагаем качественно на комплексной плоскости полюсы передаточной функции разомкнутой системы и принимаем решение, какую из трех формулировок критерия Найквиста следует применить при исследовании устойчивости по амплитудно – фазовым характеристикам разомкнутой системы (АФХ):

если все полюсы данной системы расположены в левой полуплоскости, то воспользуемся формулировкой №1 - данная замкнутая система неустойчива, так как амплитудно-фазовая характеристика разомкнутой системы охватывает точку (-1, j0).

2. Критерий Найквиста для ЛЧХ (рис. 16).

1. Если используются логарифмические частотные характеристики (ЛЧХ), то определяем количество нулевых полюсов и количество полюсов в правой части плоскости комплексной плоскости корней – m.

2. По ЛЧХ разомкнутой системы оцениваем устойчивость замкнутой системы по логарифмическому критерию Найквиста с учетом примечания к этому критерию.

m=1

Согласно критерию Найквиста, для ЛЧХ, система является условно- устойчивой, так как необходимо и достаточно, чтобы при всех значениях w, где L(w)>0, разность числа положительных и отрицательных переходов фазовой характеристики разомкнутой системы через линии ±(2k+1)p(k=0,1,2,…) равнялась m/2, где m - число полюсов с положительной вещественной частью в передаточной функции разомкнутой цепи системы.

Здесь m=1, Из этого следует, что m/2 = ½, разность переходов = => система устойчива.

Зачтено.

3. Запасы устойчивости условно-устойчивых систем.

Если устойчивость определяется по ЛЧХ условно-устойчивых систем, то для обеспечения запасов устойчивости не менее g и h необходимо, чтобы:

а) при h³L³ -hфазо-частотная характеристика удовлетворяла неравенствам θ> -180°+g или θ< -180°-g, т.е. не заходила в заштрихованную область 1 на рис. 1;

б) при -180°+g³θ³ -180°-g амплитудно-частотная характеристика удовлетворяла неравенствам L< -h или L>h, т.е. не заходила в заштрихованные области 2' и 2'' на рис. 1.

Зачтено.