
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача выпуклого программирования — это задача оптимизации, в которой целевая функция является выпуклой функцией и область допустимых решений выпукла
Задачи нелинейного программирования
Особенности
1) Условная оптимизация (наличие условий)
2) Ограничения имеют вид Неравенств или Равенств
3) ХОТЯ БЫ 1 ограничение должно быть неравенством
4) ХОТЯ БЫ 1 из функций должна быть нелинейна
| Задачи выпуклого программирования Условие Слейтера | Задачи невыпуклого программирования |
Задача выпуклого программирования — это задача оптимизации, в которой целевая функция является выпуклой функцией и область допустимых решений выпукла
В основном мы будем решать задачи, где ВСЕ ограничения – неравенства
Общая форма задач Нелинейного программирования

Функциональные ограничения
Прямые ограничения
Чтобы решить задачу, ее нужно привести к унифицированному виду

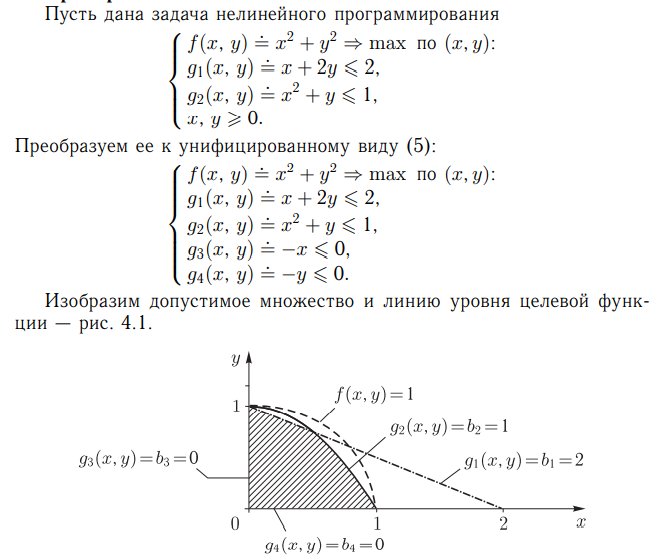
Градиенты Функций
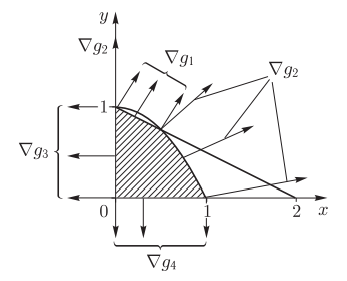
Анализ ограничений
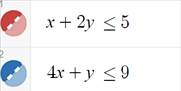
 | |||||||
 | |||||||
 | |||||||
 | |||||||
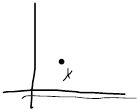
 Рисунок 1: Оба ограничения НЕактивны
Рисунок 1: Оба ограничения НЕактивны
Рисунок 2: Активное ограничение 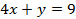
ИЩЕМ ЭКСТРЕМУМЫ
Алгоритм выявления точек локального экстремума
1) 1) Все функции должны быть непрерывно дифференциируемы в точке потенциального экстремума
2) Проверяем ККТ (составляем Функцию лагранжа и находиим потенциальные точки + множители Лямбда
Если 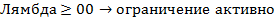
3) Проверяем Условия Якоби Для потенциальных точек
4) Если в потенциальных точке выполнено условие Якоби, то для наличия в ней условного локального экстремума необходимо, чтобы в этой точке выполнялось условие Куна–Таккера,
4) Если выполнились условие Якоби и КТ, то точка - экстремум
|
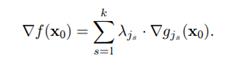 Для наличия в допустимой точке
Для наличия в допустимой точке 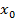 локального максимума необходимо, чтобы градиент целевой функции в данной точке мог быть представлен в виде линейной комбинации этих градиентов с неотрицательными коэффициентами, справедливо и содержится в следующей теореме
локального максимума необходимо, чтобы градиент целевой функции в данной точке мог быть представлен в виде линейной комбинации этих градиентов с неотрицательными коэффициентами, справедливо и содержится в следующей теореме
Собсна: сама сама система условий Куна Таккера (алгебраическая форма)
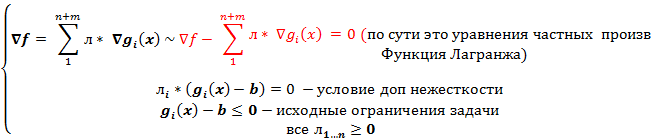
Проверить, что Точка (6,7) удовлетворяет Условиям ККТ
Целевая функция: 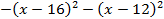
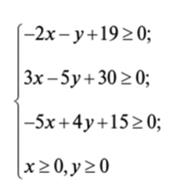
Составляем Функцию Лагранжа
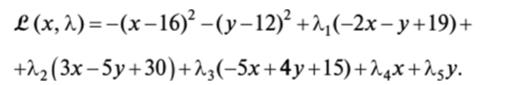
 | ||||||
 | ||||||
 | ||||||
 | ||||||


 |
+выполнены исходные ограничения
Подставляем координаты Исходной точки 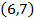 в условия
в условия
Получаем 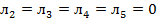
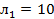
Условии теоремы КТ выполняются в точке
Задачи


|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|