
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ДИСТАНЦИОННОЕ ОБУЧЕНИЕ. Урок Производные основных элементарных функций. Повторить. Таблица производных элементарных функций
ДИСТАНЦИОННОЕ ОБУЧЕНИЕ
Урок Производные основных элементарных функций
Цели: научиться пользоваться таблицей производных элементарных функций для нахождения производных; формирование навыков вычисления производных с помощью таблицы и правил дифференцирования.
План.
1. Актуализация опорных знаний
2. Таблица производных элементарных функций и ее применение
3. Решение задач
1. Устно: Найти производную
1) 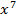 2)
2) 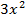 3)
3) 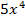 4) 10x 5) 18 6)
4) 10x 5) 18 6) 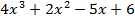
Повторить
Операция нахождения производной функции называется дифференцированием.
В результате выполнения этой операции мы по определенным правилам получаем другую функцию:
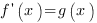
В этом равенстве 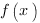 – функция, от которой мы берем производную,
– функция, от которой мы берем производную,
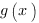 – функция, которая получается в результате этой операции.
– функция, которая получается в результате этой операции.
Элементарные функции – степенная, показательная, логарифмическая, тригонометрическая и их различные комбинации.
2. Таблица производных элементарных функций
Для того, чтобы каждый раз не искать производные элементарных функций, используя определение производной, существует таблица производных элементарных функций:
1. Производная константы равна нулю:
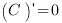
2. Производная степенной функции:
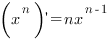
Заметим, что 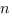 может принимать любые действительные значения.
может принимать любые действительные значения.
Примеры.
1. 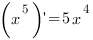
2. 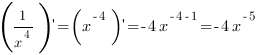
3. 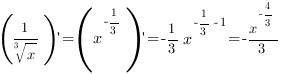
3. Производная показательной функции:
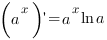
Пример.
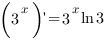
Частный случай этой формулы:

4. Производная логарифма:
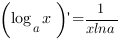
Частный случай этой формулы:
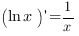
5. Производные тригонометрических функций:
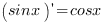
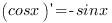
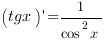
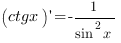
6. Производные обратных тригонометрических функций:
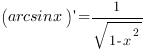
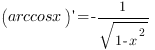
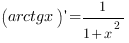
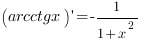
Чтобы правильно найти производную функции 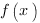 , полезно придерживаться такого алгоритма:
, полезно придерживаться такого алгоритма:
1. Выделите, какие элементарные функции входят в состав уравнения функции.
2. Отделите в явном виде коэффициенты.
3. Если возможно, упростите выражение 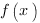 , используя свойства степени, свойства логарифмов или тригонометрические формулы в зависимости от того, какие элементарные функции входят в состав функции
, используя свойства степени, свойства логарифмов или тригонометрические формулы в зависимости от того, какие элементарные функции входят в состав функции 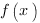
4. Вспомните, чему равны производные этих функций или посмотрите в таблице производных.
5. Обратите внимание на то, какими арифметическими действиями связаны между собой элементарные функции, которые входят в состав функции 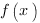 и вспомните правило, по которому находится производная суммы, разности, произведения или частного двух функций.
и вспомните правило, по которому находится производная суммы, разности, произведения или частного двух функций.
Пример 1. Найти производную функции:
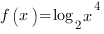
Используя свойства логарифмов, упростим выражение в правой части уравнения функции:
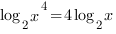
Таким образом:
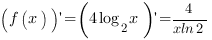
Пример 2.Найти производную функции:
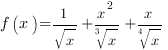
1. Упростим каждую дробь, используя свойства степени:
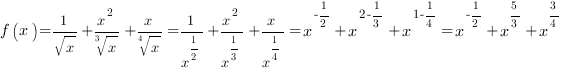
Мы видим, что наша функция представляет собой сумму степенных функций.
Следовательно:
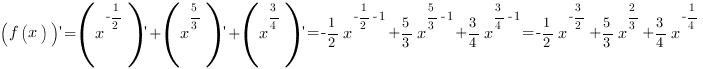
Пример 3. Найти производную функции
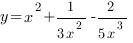
Сначала запишем каждое слагаемое в виде степени 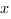 и выделим в явном виде числовые коэффициенты:
и выделим в явном виде числовые коэффициенты:
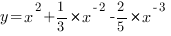
Теперь легко найти производную:
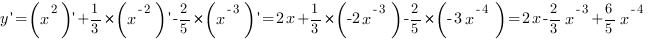
Пример 4. Найти производную функции:
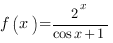
Мы видим, что наша функция представляет собой дробь, в числителе которой стоит степенная функция, а в знаменателе сумма косинуса и константы.
Найдем производную функции 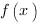 по формуле производной дроби:
по формуле производной дроби:
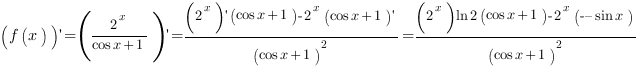
Выполнить задания.
№1. Найти производные функций:
1) 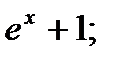 2)
2) 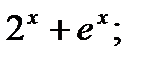 3)
3) 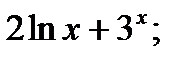 4)
4) 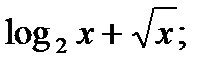 5)
5) 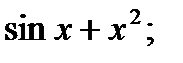
6) 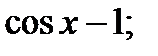 7)
7) 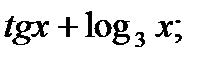 8)
8) 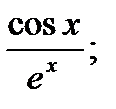 9)
9) 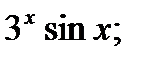
№2. Найти значение производной функции в точке 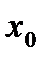
1) 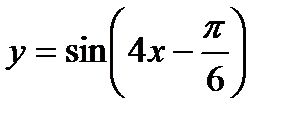 в точке
в точке 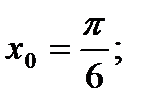 2)
2) 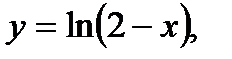
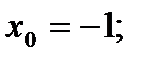
3) 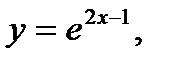
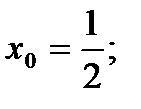 4)
4) 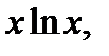
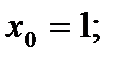 5)
5) 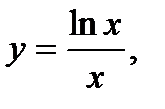
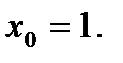
Домашнее задание. Работа с конспектом. Учить таблицу производных элементарных функций.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|