Экзаменационные вопросыпо курсу «Высшая математика»

Экзаменационные вопросыпо курсу «Высшая математика»

1. Определение комплексного числа. Арифметические операции над к.ч. Алгебраическая форма к.ч.
Сопряженные к.ч.

2. Геометрическая интерпретация и тригонометрическая форма записи к.ч.

3. Показательная форма записи к.ч. Извлечение корня из к.ч.

4. Многочлены: теорема о делении с остатком, правила деления многочленов, теорема Безу, корни
многочленов, их кратность, теорема о комплексных корнях многочлена с действительными
коэффициентами.

5. Приводимые и неприводимые многочлены над R и С. Канонические разложения над R и С. Примеры.

6. Теорема о рациональных корнях многочлена с действительными коэффициентами. Признак кратности
корня многочлена и функции.

7. Рациональные функции. Простейшие дроби. Теорема о разложении правильной рациональной дроби на
сумму простейших. Нахождение коэффициентов разложения (метод неопределенных коэффициентов,
метод произвольных значений).

8. Первообразная и неопределенный интеграл. Основные свойства неопределенного интеграла. Таблица
основных неопределенных интегралов.

9. Методы интегрирования: поднесение под знак дифференциала, замена переменной.

10. Интегрирование по частям. Типичные интегралы, берущиеся по частям. Интегралы вида 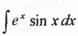и т.п.

11. Интегрирование простейших дробей и рациональных функций.

12. Интегрирование иррациональных функций вида

(подстановки Эйлера, тригонометрические подстановки).

13. Интегрирование биномиальных дифференциалов. Примеры.

14. Интегрирование тригонометрических выражений.

15. Определение определенного интеграла. Суммы Дарбу. Интегрируемые функции (теоремы).

16. Основные свойства определенного интеграла.

17. Теоремы о среднем.

18. Вычисление определенного интеграла. Интеграл с переменным верхним пределом. Формула Ньютона -
Лейбница.

19. Методы вычисления определенных интегралов: метод замены переменных, интегрирование по частям.
Интегрирование периодических, четных и нечетных функций.

20. Вычисление площадей плоских фигур с помощью определенного интеграла (в декартовой и полярной
системах координат).

21. Вычисление объемов тел с помощью определенного интеграла (по известным поперечным сечениям, объем
тела вращения).

22. Вычисление длины дуги кривой с помощью определенного интеграла (в декартовой и полярной системах
координат).

23. Вычисление площади поверхности вращения с помощью определенного интеграла.

24. Физические приложения определенного интеграла (работа переменной силы, сила давления жидкости на
вертикальную пластину и другие).

25. Несобственные интегралы с бесконечными пределами (НИ-1). Определение, признаки сравнения,
эталонный НИ-1, абсолютная и условная сходимость. Главное значение НИ-1.

26. Несобственные интегралы от неограниченных функций (НИ-П). Определение, признаки сравнения,
эталонный НИ-Н. Главное значение НИ-П.

27. Определение функции многих переменных. Линии и поверхности уровня.

28. Предел функции многих переменных: предел функции в точке, повторные пределы, предел в данном
направлении.

29. Непрерывность функций многих переменных. Свойства непрерывных функций.

30. Частные производные первого порядка функции многих переменных. Их геометрический смысл.

31. Полный дифференциал функции многих переменных. Частный дифференциал. Необходимое условие
дифференцируемости. Достаточное условие дифференцируемости. Использование полного дифференциала
для приближенных вычислений значений функции.

32. Производная сложной функции нескольких переменных. Полная производная. Дифференцирование
неявных функций.

33. Производная по направлению. Теорема о ее вычислении. Теорема о возрастании-убывании функции в
данном направлении. Градиент.

34. Касательная плоскость и нормаль к поверхности.

35. Частные производные высших порядков. Теорема о равенстве смешанных производных. Признак полного
дифференциала.

36. Дифференциалы высших порядков. Неинвариантность их формы.

37. Формула Тейлора для функций многих переменных.

38. Локальный экстремум функций многих переменных. Теорема о необходимом и теоремы о достаточных
условиях локального экстремума. Глобальный экстремум.

39. Условный экстремум функций многих переменных. Метод множителей Лагранжа.

40. Определение двойного интеграла и его основные свойства.

41. Вычисление двойного интеграла.

42. Замена переменных в двойном интеграле.

43. Определение и основные свойства тройного интеграла.

44. Вычисление тройного интеграла.

45. Замена переменных в тройном интеграле.

46. Криволинейный интеграл первого рода (КРИ-1).

47. Криволинейный интеграл второго рода (КРИ-И).

48. Связь между КРИ-I и КРИ-П.

49. Формула Грина (связь между двойными и криволинейными интегралами).

50. Условия независимости КРИ-П от пути интегрирования.

51. Двусторонние поверхности. Площадь поверхности.

52. Поверхностные интегралы первого типа (определение, вычисление).

53. Поверхностные интегралы второго типа (нормаль к поверхности, определение ПИ-П, вычисление).

54. Связь между ПИ-I и ПИ-П.

55. Формула Остроградского (связь между тройными и поверхностными интегралами).

56. Формула Стокса (связь между криволинейными и поверхностными интегралами).

57. Скалярные и векторные поля (основные понятия и определения).

58. Поток вектора через поверхность. Его вычисление в случаях явно, неявно и параметрически заданной
поверхности.

59. Поток вектора через замкнутую поверхность. Источники. Стоки. Дивергенция и ее физический смыся.
Формула Остроградского в векторной форме.

60. Циркуляция вектора. Ротор.

61. Потенциальные и соленоидальные векторные поля.

62. Обыкновенные дифференциальные уравнения: общие понятия и определения. Задача Коши.

63. Уравнения с разделяющимися переменными; однородные дифференциальные уравнения первого порядка;
уравнения, приводящиеся к ним.

64. Линейные обыкновенные дифференциальные уравнения первого порядка. Метод вариации произвольной
постоянной (Лагранжа), Метод интегрирующего множителя (Эйлера). Уравнение Бернулли.

65. Уравнения в полных дифференциалах. Интегрирующий множитель.

66. Обыкновенные дифференциальные уравнения высших порядков. Общие понятия и определения i
(уравнение, решение, общее решение, задача Коши, краевая задача).

67. Уравнения n-го порядка, интегрируемые в квадратурах и допускающие понижение порядка.

68. Линейные дифференциальные уравнения высших порядков. Общие понятия и определения. Линейные
однородные уравнения n-го порядка. Свойства решений. Линейная зависимость, фундаментальная система
решений.

69. Линейные однородные дифференциальные уравнения с постоянными коэффициентами. Метод Эйлера.

70. Линейные неоднородные дифференциальные уравнения n-го порядка. Принцип суперпозиции. Метод
вариации произвольных постоянных.

71. Линейные неоднородные дифференциальные уравнения n-го порядка с постоянными коэффициентами и со
специальной правой частью.

72. Системы обыкновенных дифференциальных уравнений (общие понятия и определения). Связь между
системами ОДУ и уравнениями высших порядков.

73. Линейные однородные системы ОДУ. Свойства их решений. Фундаментальная система решений. Метод
Эйлера решения линейных однородных систем с постоянными коэффициентами.

74. Линейные неоднородные системы ОДУ с постоянными коэффициентами. Метод вариации произвольных
постоянных.