Контакты

Случайная статья

Тема 2.1. Основы тригонометрии.

Тема 2.1. Основы тригонометрии.

Урок 1. Синус, косинус, тангенс, котангенс произвольного угла. Нахождение синусов и косинусов произвольных углов.

Домашнее задание

Выучить определения и формулы тригонометрии!

Решить следующие задачи: №1(б-г), №2(б), №3(в-г), №4(б-г), №7(б-г), №8.

Указания!

№1 а) Выразите в радианной мере величины углов: , .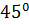

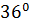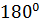Для перевода градусной меры углов в радианную воспользуемся равенством

.

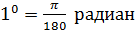Тогда .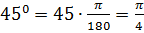

Аналогично остальные примеры:

.

.

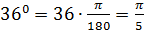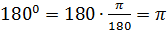№2. Выразите в градусной мере величины углов

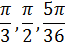
Теперь воспользуемся формулой 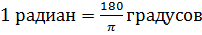, получим

.

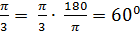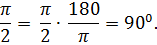
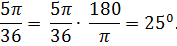
№3. Найдите числовое значение выражения:

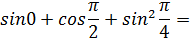
Воспользуемся таблицей значений тригонометрических функций, которая находится на странице 7, получим

.

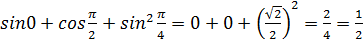№4. Существуют ли числа 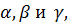для которых

.

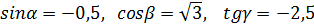!!! Надо запомнить, что область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса - вся числовая прямая, то есть эти функции могут принимать любые значения. !!!

Т.к. 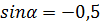, а 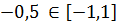, то число 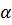существует.

Т.к.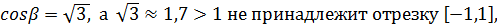

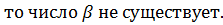
Т.к. 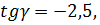а область значений тангенса – это вся числовая прямая, то число 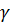существует.

№5. Могут ли синус и косинус одного и того же числа быть равными соответственно:

А) .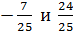

Нам известно основное тождество тригонометрии

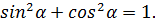
Для решения нашей задачи, положим 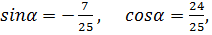тогда

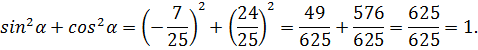
Ответ: могут.

№7. Найдите значения других трех основных тригонометрических функций, если:

А) .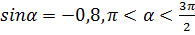

Опять воспользуемся основным тождеством тригонометрии

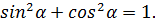
Подставим в эту формулу то, что нам известно по условию :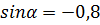

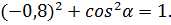
Отсюда

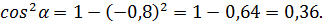
Т.к. 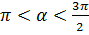, то 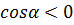, т.к. имеет отрицательные значения в третьей четверти (см. ниже рисунок косинуса на единичной окружности).

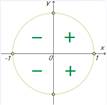
Тогда из равенства 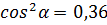, выберем только отрицательный косинус, т.е. .

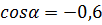Найдем тангенс и котангенс числа 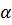, а они связаны следующими формулами:

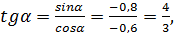а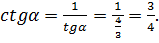

№8. Упростите выражение

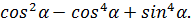
Применим формулу разности квадратов

.

.

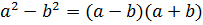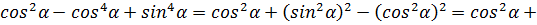
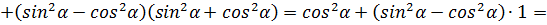
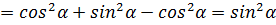© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.