
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема 1.2. Логарифмы.. Урок 2. Свойства логарифмов. Переход к новому основанию. Решение задач.. Домашнее задание. Переход к новому основанию
Тема 1.2. Логарифмы.
Урок 2. Свойства логарифмов. Переход к новому основанию. Решение задач.
Продолжаем изучать тему «Логарифмы».
№491
a) 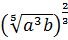 .
.
Прологарифмируем это выражение по основанию 3:
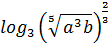
теперь воспользуемся свойствами логарифмов и преобразуем это выражение
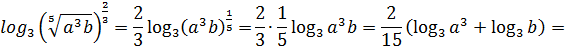
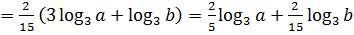 .
.
№492
а) 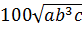 .
.
Прологарифмируем это выражение по основанию 10:
Логарифм с основанием 10 обозначается lg, поэтому
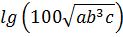
теперь воспользуемся свойствами логарифмов и преобразуем это выражение
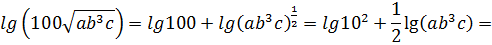
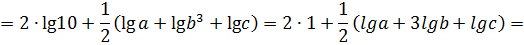
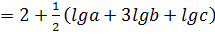 .
.
№495. Вычислите
а) 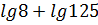
Воспользуемся свойствами логарифмов:
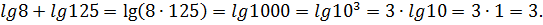
№497. Найдите х, если
а) 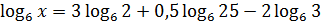 .
.
Воспользуемся свойствами логарифмов и преобразуем правую часть:

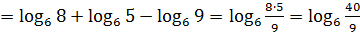 .
.
Отсюда получаем: 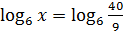 , а, следовательно,
, а, следовательно, 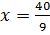 .
.
Домашнее задание
Продолжаем учить определение и свойства логарифмов! В ваших книгах по математике прочитать параграф 37 (в зависимости от года выпуска книги это где-то 233-235 стр)
Решить следующие задачи: №491 (б-г), №492 (б-г), №495 (б-г), №496, №497(б-г).
Переход к новому основанию
Когда требуется осуществить переход к новому основанию логарифма, пользуются одним из свойств логарифмов —
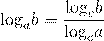
где 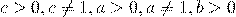 .
.
(Для запоминания этой формулы удобно воспользоваться следующей ассоциацией: то, что вверху, идёт вверх, то, что внизу — идёт вниз.
b, стоящее вверху, под знаком логарифма, записываем снова вверху, в числителе, под знак логарифма с новым основанием.
a, стоящее внизу, в основании логарифма, записываем вниз, в знаменателе, под знак логарифма с новым основанием).
Примеры перехода к новому основанию логарифма:
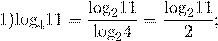
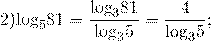
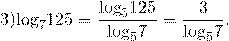
Перейти можно к любому новому основанию (положительному и отличному от единицы).
В том числе, любой логарифм можно представить в виде частного десятичных логарифмов:
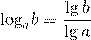
или в виде частного натуральных логарифмов:
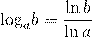
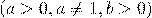
Например,
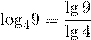
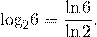
Частный случай этой формулы —
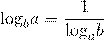
позволяет изменить основание логарифма на число, стоящее под знаком логарифма.
Еще одно свойство логарифма —
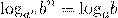
— дает возможность изменить основание логарифма в случае, когда оно может быть представлено в виде степени.
Пример 1.Вычислите:
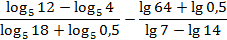
Решение.Разность логарифмов с одинаковым основанием – это логарифм частного, а сумма логарифмов с одинаковым основанием – логарифм произведения. А у нас в числителях и знаменателях стоят логарифмы с одинаковыми основаниями.
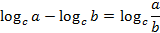
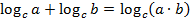
Применяя эти свойства, получаем:
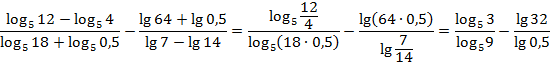
Согласно формуле перехода к новому основанию
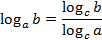 :
:
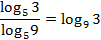
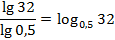
Следовательно, 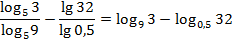
Из основания логарифма показатель степени 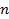 выносится за знак логарифма как
выносится за знак логарифма как  , а из подлогарифмического выражения – как
, а из подлогарифмического выражения – как 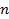 , то есть:
, то есть:

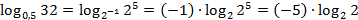
Следовательно: 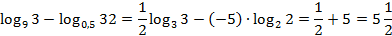
Ответ: 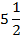 .
.
Пример 2.Вычислите:
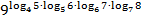
Решение
Нам известно следствие из формулы перехода к новому основанию:
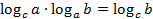
С помощью этой формулы преобразуем показатель степени в данном выражении:
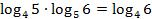
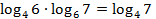
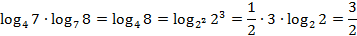
Таким образом:
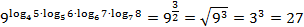
Ответ: 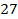 .
.
Пример 3.Вычислите:
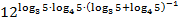
Решение.Преобразуем показатель степени, избавившись от минус первой степени:
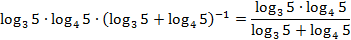
Приведем всё к одному основанию (в данном случае к 5), воспользовавшись следствием из формулы перехода к новому основанию
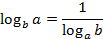
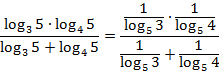
Домножим числитель и знаменатель на 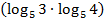 :
:
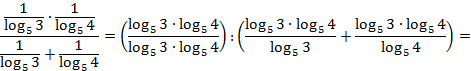
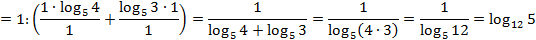
Следовательно:
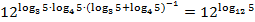
Применим основное логарифмическое тождество:
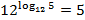
Ответ: 5.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|