Лабораторная работа №1.4. Исследование дифференцирующих и интегрирующих цепей». Подготовка к работе

Отчет

По лабораторной работе 1.4

Вакуленко Евгения

ИВТ-1

Макет №5

Лабораторная работа №1.4

«Исследование дифференцирующих и интегрирующих цепей»

Цель: изучить принцип действия дифференцирующих и интегрирующих цепей.

Оборудование: макет (номиналы элементов указываются преподавателем), осциллограф, генератор синусоидальных и прямоугольных сигналов, вольтметр переменного напряжения.

Подготовка к работе

1.Изучить схемы, принцип действия, назначение исследуемых цепей.
2. Рассчитать для RC-цепи и для RL-цепи сопротивления «3» (переключатель S6).

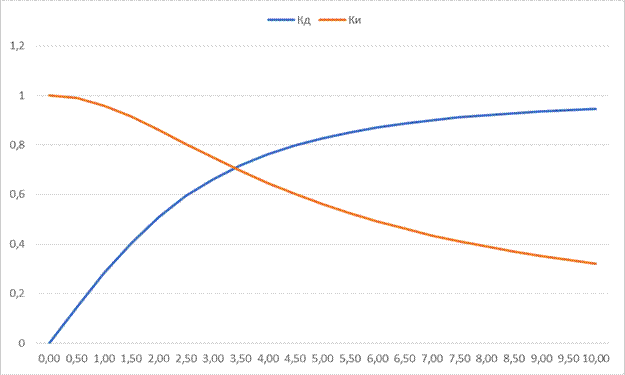
3. Рассчитать для диффференцирующей и интегрирующей цепей зависимость коэффициента передачи от частоты, полученные значения занести в таблицу и построить по ним графики.

τ_ц= RC = 4700*0,01*10^-6= 4,7 * 10^-5

ω = 2πf

K_д =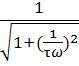

K_и =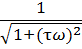

RC-цепь:

f, кГц		0,5		1,5		2,5		3,5		4,5
Кд		0,145	0,283	0,404	0,508	0,593	0,662	0,718	0,763	0,798	0,827
Ки		0,989	0,959	0,914	0,861	0,804	0,748	0,695	0,646	0,601	0,560
f, кГц	5,5		6,5		7,5		8,5		9,5		-
Кд	0,851	0,870	0,886	0,900	0,911	0,920	0,928	0,935	0,941	0,947	-
Ки	0,524	0,491	0,462	0,435	0,411	0,389	0,370	0,352	0,335	0,320	-

Для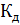
1. f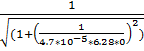(0) = = 0

2.f(0,5) 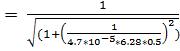= 0.145 (Гц)

3.f(1) = 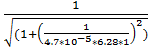= 0.283 (Гц)

4.f(1,5) = 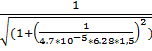= 0,404 (Гц)

5.f(2) = = 0,508 (Гц)

6.f(2,5) = 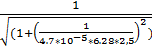= 0,593 (Гц)

7.f(3) = 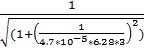= 0,662 (Гц)

8.f(3,5) = 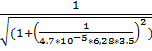= 0,718 (Гц)

9.f(4) = = 0,763 (Гц)

10.f(4,5) 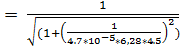= 0,798 (Гц)

11.f(5) = 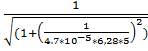= 0,827 (Гц)

12.f(5,5) = 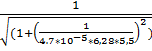= 0,851 (Гц)

13.f(6) = 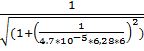=0,870 (Гц)

14.f(6,5) = 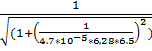= 0,886 (Гц)

15.f(7) = = 0,900 (Гц)

16.f(7,5) = 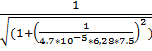= 0,911(Гц)

17.f(8) = 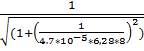= 0,920 (Гц)

18.f(8,5) = 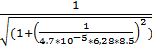= 0,928(Гц)

19.f(9) = = 0,935 (Гц)

20.f(9,5) 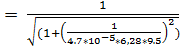= 0,941 (Гц)

21.f(10) = 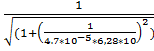=0,947 (Гц)

Для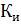

1.f(0) = 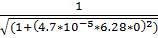=1

2.f(0.5) = 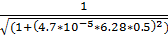= 0.989

3.f(1) = 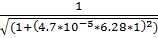= 0.959

4.f(1.5)= 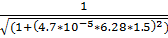= 0.914

5.f(2)= 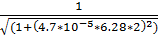= 0.861

6.f(2.5) ) = 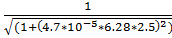= 0.804

7.f(3) = 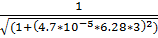=0.748

8.f(3.5) = 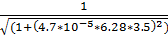= 0.695

9.f(4) = 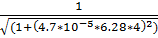= 0.646

10.f(4.5)= 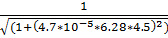= 0.601

11.f(5)= 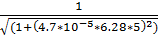= 0.560

12.f(5.5) = = 0.524

13. f(6) = 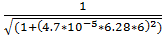= 0.491

14.f(6.5) = 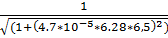=0.462

15.f(7) = 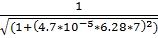= 0.435

16.f(7.5) = 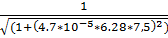= 0.411

17.f(8)= 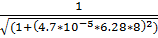= 0.389

18.f(8.5)= 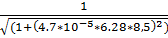= 0.370

19.f(9) ) = 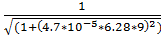= 0.352

20.f(9.5) = 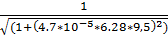=0.335

21.f(10) = 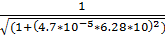= 0.320

RL-цепь:

τ_ц = = = 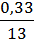2,538 * 10^-5

ω = 2πf

K_д =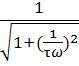

K_и =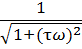

f, кГц		0,5		1,5		2,5		3,5		4,5
Кд		0,079	0,157	0,232	0,303	0,370	0,431	0,487	0,537	0,582	0,623
Ки		0,996	0,987	0,972	0,952	0,928	0,902	0,873	0,843	0,812	0,782
f, кГц	5,5		6,5		7,5		8,5		9,5		-
Кд	0,659	0,691	0,719	0,744	0,767	0,786	0,804	0,820	0,834	0,847	-
Ки	0,751	0,722	0,694	0,667	0,641	0,617	0,593	0,571	0,551	0,531	-

Для К_д

1. f (0) = 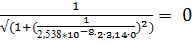(Гц)

2. f (0,5) =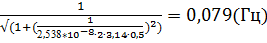

3. f (1) =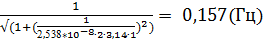

4. f (1,5) =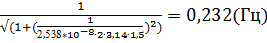

5. f (2) = 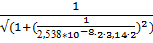= 0,303(Гц)

6. f (2,5) =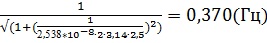

7. f (3) =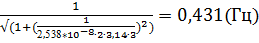

8. f (3,5) =

9. f (4) =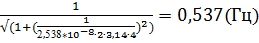

10. f (4,5) =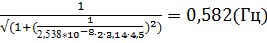

11. f (5) =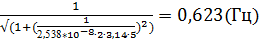

12. f (5,5) =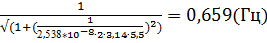

13. f (6) = 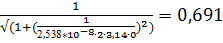(Гц)

14. f (6,5) =

15. f (7) =

16. f (7,5) =

17. f (8) =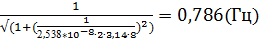

18. f (8,5) = 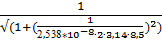= 0,804(Гц)

19. f (9) =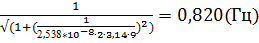

20. f (9,5) =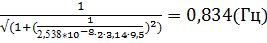

21. f (10) = 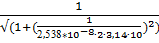= 0,847(Гц)

Для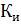

1.f(0) = 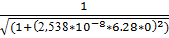=1

2.f(0.5) = = 0.996

3.f(1) = 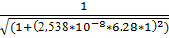= 0.987

4.f(1.5)= 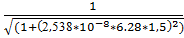= 0.972

5.f(2)= 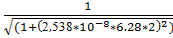= 0.952

6.f(2.5) ) = = 0.928

7.f(3) = 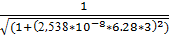=0.902

8.f(3.5) = = 0.873

9.f(4) = 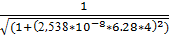= 0.843

10.f(4.5)= 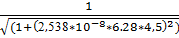= 0.812

11.f(5)= = 0.782

12.f(5.5) = 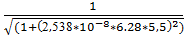= 0.751

13. f(6) = 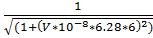= 0.722

14.f(6.5) = 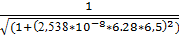=0.694

15.f(7) = = 0.667

16.f(7.5) = 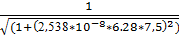= 0.641

17.f(8)= = 0.617

18.f(8.5)= = 0.593

19.f(9) ) = = 0.571

20.f(9.5) = 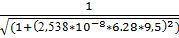=0.551

21.f(10) = 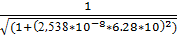= 0.531

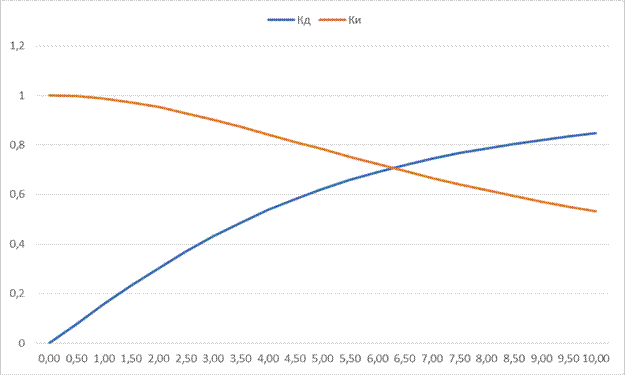
Вывод: на этой лабораторной работе мы изучили принцип действия дифференцирующих и интегрирующих цепей. Научились рассчитывать коэффициент передачи и построили график зависимости коэффициента передачи от частоты. Согласно теоретическим данным, график построен верно.

Контрольные вопросы
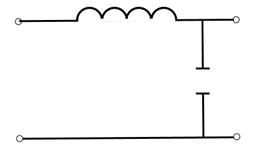
1.Дифференцирующая цепь называется цепь, в которой мгновенное значение напряжения на выходе прямо пропорционально дифференциалу входного напряжения. U_вых(t) ~ d/dt U_вх(t).

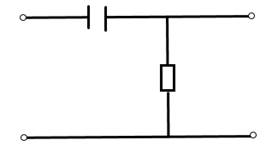2. Простейшая дифференцирующая цепь.

Физические процессы: во время включения входного сигнала - процесс зарядки конденсатора, т.е. по цепи проходит ток зарядки и напряжение на выходе максимально. По мере протекания процесса зарядки ток уменьшается по экспоненциальному закону до нулевого значения, уменьшается напряжение на выходе. При отключении сигнала = аналогичный процесс, но вызван разрядкой конденсатора.

3. Напряжение необходимо снимать с сопротивления R.

4.Уменьшить постоянную времени τ = RC.

6. Уменьшится, т.к. при уменьшении частоты входного сигнала дифференцирующей цепи уменьшится частотный коэффициент передачи.

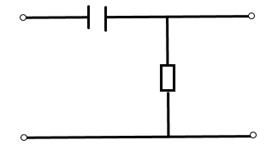
7. Интегрирующей цепью называется цепь, у которой мгновенное значение напряжения на выходе прямо пропорционально интегралу входного напряжения U_вых(t) ~ ∫U_вх(t)dt.

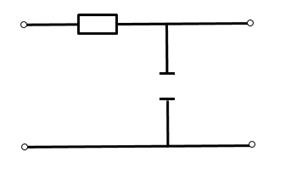8. Простейшая интегрирующая цепь.

Физические процессы: при воздействии на вход цепи периодических последовательных прямоугольных импульсов при выполнении условия интегрирования: τ >> T_u, в момент поступления импульса на вход цепи всё напряжение оказывается приложенным к резистору, а напряжение на конденсаторе равно нулю. Далее напряжение на конденсаторе медленно возрастает, т.к. происходит медленный заряд конденсатора по экспоненциальному закону. К моменту окончания входного импульса напряжение на конденсаторе не успевает достигнуть значение напряжения U_т. После окончания входного импульса конденсатор так же медленно разряжается. Таким образом на ёмкостном выходе цепи будет выделяться растянутые импульсы, имеющие форму экспоненциальной цепи.

9. Чем больше величины номиналов RC, тем меньше переменная составляющая на выходе, тем более точной будет кривая функции.

10.

11. K = 1 / √ 1 +(1/(τ2πf)²) - для дифференцирующей цепи, чем больше частота, тем больше коэффициент передачи.

K = 1 / √ 1 +(τ2πf)² - для интегрирующей цепи, чем больше частота, тем меньше коэффициент передачи.

12. Определяется соотношением τ_u = 3τ, T_u_вых. = (3...5) τ.

Если τ <<T_u, то на выходе два остроконечных импульса противоположной полярности. Длительность каждого на уровне 0.1 от максимального значения.

13. Дифференцирующие (укорачивающие) цепи применяются для развязки по постоянному току (они не пропускают постоянное напряжение, а переменный сигнал проходит), либо для развязки сигналов, сильно отличающихся по частоте. Предназначены для формирования импульсов малой длительности.

Интегрирующие (сглаживающие) цепи применяются для подавления высокочастотных помех и сигналов; также называется удлиняющей. Предназначены для формирования импульсов большой длительности, фильтра низких частот.
14.

15.