
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение: 1) Функция определена и непрерывна на всей числовой прямой: . Это очень хорошо, отпадают вертикальные асимптоты.
Пример 1
Исследовать функцию и по результатам исследования построить график.
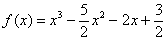
Решение: 1) Функция определена и непрерывна на всей числовой прямой: . Это очень хорошо, отпадают вертикальные асимптоты.
Проверим функцию на чётность/нечётность:
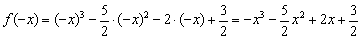
После чего следует шаблонная отписка:
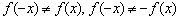 , значит, данная функция не является чётной или нечётной.
, значит, данная функция не является чётной или нечётной.
Очевидно, что функция непериодическая.
2) Асимптоты, поведение функции на бесконечности.
Так как функция непрерывна на 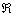 , то вертикальные асимптоты отсутствуют.
, то вертикальные асимптоты отсутствуют.
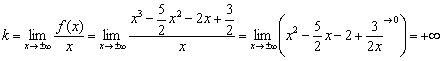
Нет и наклонных асимптот.
Примечание: напоминаю, что 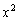 более высокого порядка роста, чем
более высокого порядка роста, чем 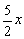 , поэтому итоговый предел равен именно «плюс бесконечности».
, поэтому итоговый предел равен именно «плюс бесконечности».
Выясним, как ведёт себя функция на бесконечности:
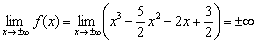
Иными словами, если идём вправо, то график уходит бесконечно далеко вверх, если влево – бесконечно далеко вниз. Да, здесь тоже два предела под единой записью. Если у вас возникли трудности с расшифровкой знаков 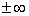 , пожалуйста, посетите урок о бесконечно малых функциях.
, пожалуйста, посетите урок о бесконечно малых функциях.
Таким образом, функция не ограничена сверху и не ограничена снизу. Учитывая, что у нас нет точек разрыва, становится понятна и область значений функции: 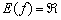 – тоже любое действительное число.
– тоже любое действительное число.
3) Нули функции и интервалы знакопостоянства.
Сначала найдём точку пересечения графика с осью ординат. Это просто. Необходимо вычислить значение функции при 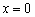 :
:
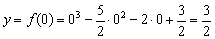
Полтора над уровнем моря.
Чтобы найти точки пересечения с осью 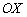 (нули функции) требуется решить уравнение
(нули функции) требуется решить уравнение 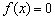 , и тут нас поджидает неприятный сюрприз:
, и тут нас поджидает неприятный сюрприз:
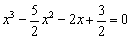
В конце притаился свободный член, который существенно затрудняет задачу.
Такое уравнение имеет, как минимум, один действительный корень, и чаще всего этот корень иррационален. В худшей же сказке нас поджидают три поросёнка. Уравнение разрешимо с помощью так называемых формул Кардано, но порча бумаги сопоставима чуть ли не со всем исследованием. В этой связи разумнее устно либо на черновике попытаться подобрать хотя бы один целый корень. Проверим, не являются ли оными числа 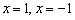 :
:
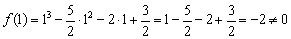 – не подходит;
– не подходит;
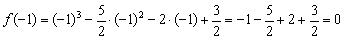 – есть!
– есть!
Здесь повезло. В случае неудачи можно протестировать ещё 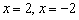 и
и 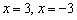 , а если и эти числа не подошли, то шансов на выгодное решение уравнения, боюсь, очень мало. Тогда пункт исследования лучше полностью пропустить – авось станет что-нибудь понятнее на завершающем шаге, когда будут пробиваться дополнительные точки. И если таки корень (корни) явно «нехорошие», то об интервалах знакопостоянства лучше вообще скромно умолчать да поаккуратнее выполнить чертёж.
, а если и эти числа не подошли, то шансов на выгодное решение уравнения, боюсь, очень мало. Тогда пункт исследования лучше полностью пропустить – авось станет что-нибудь понятнее на завершающем шаге, когда будут пробиваться дополнительные точки. И если таки корень (корни) явно «нехорошие», то об интервалах знакопостоянства лучше вообще скромно умолчать да поаккуратнее выполнить чертёж.
Однако у нас есть красивый корень 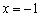 , поэтому делим многочлен
, поэтому делим многочлен 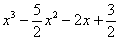 на
на 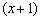 без остатка:
без остатка:
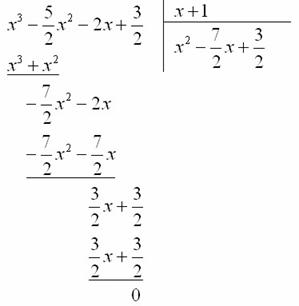
Алгоритм деления многочлена на многочлен детально разобран в первом примере урока Сложные пределы.
В итоге левая часть исходного уравнения 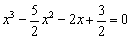 раскладывается в произведение:
раскладывается в произведение:
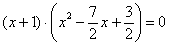
А теперь немного о здоровом образе жизни. Я, конечно же, понимаю, что квадратные уравнения нужно решать каждый день, но сегодня сделаем исключение: уравнение 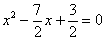 имеет два действительных корня
имеет два действительных корня 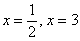 .
.
На числовой прямой отложим найденные значения 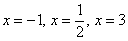 и методом интервалов определим знаки функции:
и методом интервалов определим знаки функции:

Таким образом, на интервалах 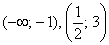 график расположен
график расположен
ниже оси абсцисс 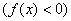 , а на интервалах
, а на интервалах 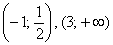 – выше данной оси
– выше данной оси 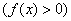 .
.
4) Возрастание, убывание и экстремумы функции.
Найдём критические точки:
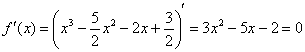
Данное уравнение имеет два действительных корня 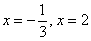 . Отложим их на числовой прямой и определим знаки производной:
. Отложим их на числовой прямой и определим знаки производной:

Следовательно, функция возрастает на 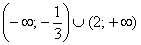 и убывает на
и убывает на 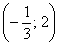 .
.
В точке 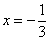 функция достигает максимума:
функция достигает максимума: 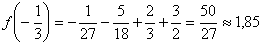 .
.
В точке 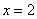 функция достигает минимума:
функция достигает минимума: 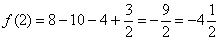 .
.
5) Выпуклость, вогнутость и точки перегиба.
Найдём критические точки второй производной:
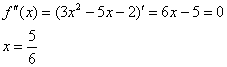
Определим знаки 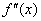 :
:

График функции является выпуклым на 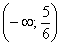 и вогнутым на
и вогнутым на 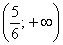 . Вычислим ординату точки перегиба:
. Вычислим ординату точки перегиба: 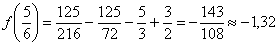 .
.
Практически всё прояснилось.
6) Осталось найти дополнительные точки, которые помогут точнее построить график и выполнить самопроверку. В данном случае их мало, но пренебрегать не будем:

Выполним чертёж:
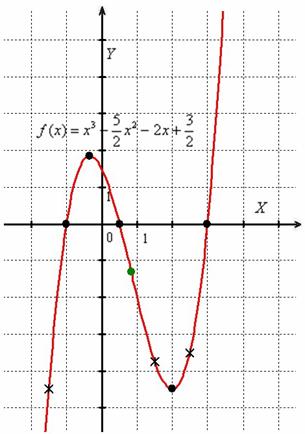
Зелёным цветом отмечена точка перегиба, крестиками – дополнительные точки. График кубической функции симметричен относительно своей точки перегиба, которая всегда расположена строго посередине между максимумом и минимумом.
Для самостоятельного решения:
Пример 2
Исследовать функцию и построить график.
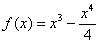
Тут всё быстрее и веселее, примерный образец чистового оформления в конце урока.
Пример 3
Методами дифференциального исчисления исследовать функцию и на основании результатов исследования построить её график.
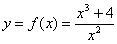
Решение: первый этап исследования не отличается чем-то примечательным, за исключением дырки в области определения:
1) Функция определена и непрерывна на всей числовой прямой кроме точки 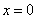 , область определения:
, область определения: 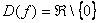 .
.
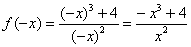
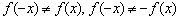 , значит, данная функция не является четной или нечетной.
, значит, данная функция не является четной или нечетной.
Очевидно, что функция непериодическая.
График функции представляет собой две непрерывные ветви, расположенные в левой и правой полуплоскости – это, пожалуй, самый важный вывод 1-го пункта.
2) Асимптоты, поведение функции на бесконечности.
а) С помощью односторонних пределов исследуем поведение функции вблизи подозрительной точки, где явно должна быть вертикальная асимптота:
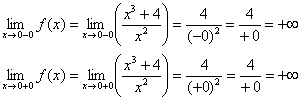
Действительно, функции терпит бесконечный разрыв в точке 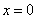 ,
,
а прямая 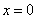 (ось
(ось 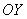 ) является вертикальной асимптотой графика
) является вертикальной асимптотой графика 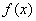 .
.
б) Проверим, существуют ли наклонные асимптоты:
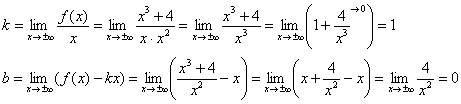
Да, прямая 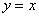 является наклонной асимптотой графика
является наклонной асимптотой графика 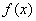 , если
, если 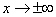 .
.
Пределы 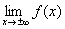 анализировать смысла не имеет, поскольку и так понятно, что функция в обнимку со своей наклонной асимптотой не ограничена сверху и не ограничена снизу.
анализировать смысла не имеет, поскольку и так понятно, что функция в обнимку со своей наклонной асимптотой не ограничена сверху и не ограничена снизу.
3) Точки пересечения графика с координатными осями, интервалы знакопостоянства функции.
График функции не пересекает ось 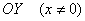 .
.
С осью 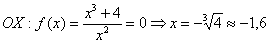
Методом интервалов определим знаки 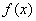 :
:

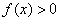 , если
, если 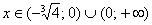 ;
;
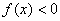 , если
, если 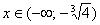 .
.
4) Возрастание, убывание, экстремумы функции.
В рассматриваемом примере числитель почленно делится на знаменатель, что очень выгодно для дифференцирования:

Собственно, это уже проделывалось при нахождении асимптот.
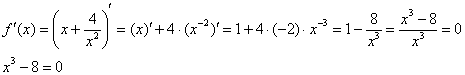
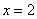 – критическая точка.
– критическая точка.
Определим знаки 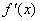 :
:

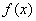 возрастает на
возрастает на 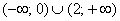 и убывает на
и убывает на 
В точке 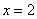 функция достигает минимума:
функция достигает минимума: 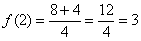 .
.
5) Выпуклость, вогнутость, перегибы графика.
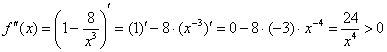 , значит, график функции является вогнутым на всей области определения.
, значит, график функции является вогнутым на всей области определения.
Отлично – и чертить ничего не надо.
Точки перегиба отсутствуют.
Вогнутость согласуется с Выводом № 3, более того, указывает, что на бесконечности (и там и там) график функции расположен выше своей наклонной асимптоты.
6) Добросовестно приколотим задание дополнительными точками. Вот здесь придётся изрядно потрудиться, поскольку из исследования нам известны только две точки.

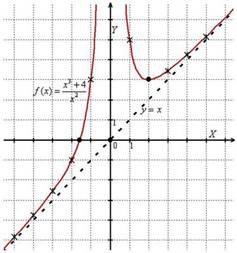
Пример 4
Методами дифференциального исчисления исследовать функцию и построить её график.
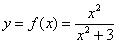
Это пример для самостоятельного решения. В нём самоконтроль усиливается чётностью функции – график симметричен относительно оси 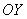 , и если в вашем исследовании что-то противоречит данному факту, ищите ошибку.
, и если в вашем исследовании что-то противоречит данному факту, ищите ошибку.
Решения и ответы:
Пример 2: Решение: проведём исследование функции:
1) Функция определена и непрерывна на всей числовой прямой, 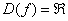 .
.

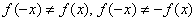 , значит, данная функция не является четной или нечетной.
, значит, данная функция не является четной или нечетной.
Функция непериодическая.
2) Асимптоты графика, поведение функции на бесконечности.
Так как функция непрерывна на 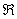 , то вертикальные асимптоты отсутствуют.
, то вертикальные асимптоты отсутствуют.
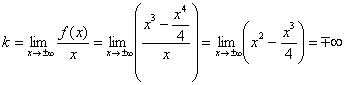 , значит, наклонные асимптоты также отсутствуют.
, значит, наклонные асимптоты также отсутствуют.
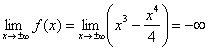 , функция не ограничена снизу.
, функция не ограничена снизу.
3) Точки пересечения графика с координатными осями, интервалы знакопостоянства функции.
График 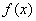 проходит через начало координат.
проходит через начало координат.
С осью 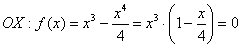
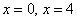
Определим знаки 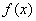 :
:

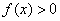 , если
, если 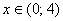 ,
,
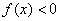 , если
, если 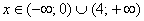 .
.
4) Возрастание, убывание, экстремумы функции.
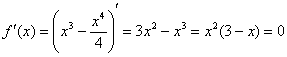
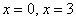 – критические точки.
– критические точки.
Определим знаки 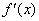 :
:

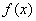 возрастает на
возрастает на 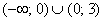 и убывает на
и убывает на  .
.
В точке 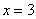 функция достигает максимума:
функция достигает максимума: 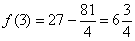
5) Выпуклость, вогнутость, перегибы графика.
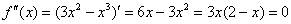
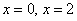 – критические точки.
– критические точки.
Определим знаки 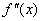 :
:

График функции является выпуклым на 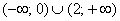 и вогнутым на
и вогнутым на  .
.
В обеих критических точках существуют перегибы графика.
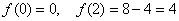
6) Найдем дополнительные точки:

Выполним чертёж:
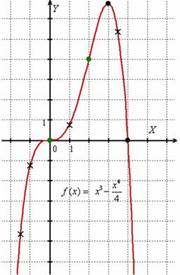
Пример 4: Решение: проведем исследование функции:
1) Функция определена и непрерывна на всей числовой прямой, 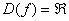 .
.
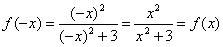
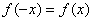 , значит, данная функция является четной, ее график симметричен относительно оси ординат.
, значит, данная функция является четной, ее график симметричен относительно оси ординат.
Очевидно, что функция непериодическая.
2) Асимптоты, поведение функции на бесконечности.
Так как функция непрерывна на всей числовой прямой, то вертикальные асимптоты отсутствуют.
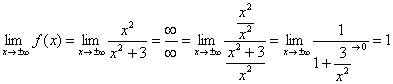
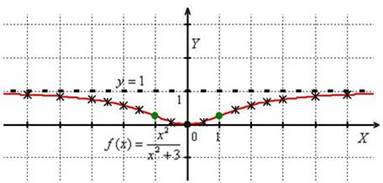
Прямая 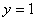 является горизонтальной асимптотой для графика
является горизонтальной асимптотой для графика 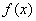 при
при 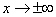 .
.
3) Точки пересечения графика с координатными осями, интервалы знакопостоянства функции.
График функции проходит через начало координат.
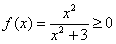 на всей области определения.
на всей области определения.
4) Возрастание, убывание, экстремумы функции.
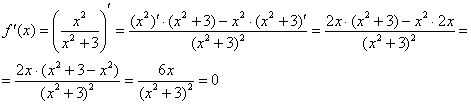
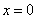 – критическая точка.
– критическая точка.
Определим знаки 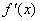 :
:

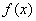 возрастает на
возрастает на  и убывает на
и убывает на  .
.
В точке 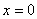 функция достигает минимума:
функция достигает минимума: 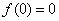 .
.
5) Выпуклость, вогнутость, перегибы графика.
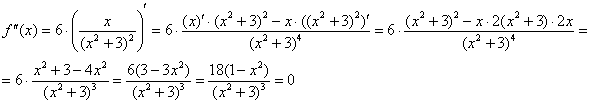
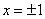 – критические точки.
– критические точки.
Определим знаки 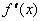 :
:

График 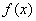 является выпуклым на
является выпуклым на 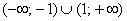 и вогнутым на
и вогнутым на 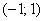 .
.
В обеих критических точках существуют перегибы графика: 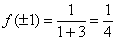 .
.
6) Найдем дополнительные точки и выполним чертёж:

Автор: Емелин Александр
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|