Контакты

Случайная статья

Формула Грина

Формула Грина

Пусть в плоскости XOY дана ограниченная замкнутым контуром L область D.

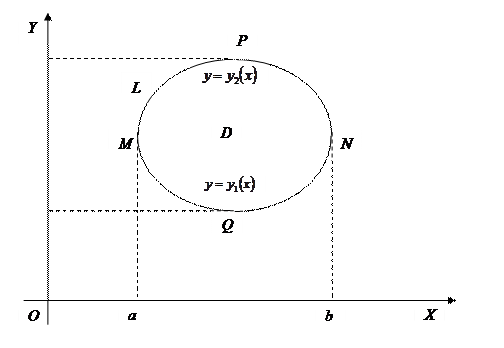
Пусть область D ограничена снизу кривой 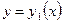, сверху кривой 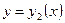, где 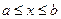. Пусть в области D заданы непрерывные функции X(x;y) и Y(x;y), имеющие непрерывные частные производные. Рассмотрим интеграл

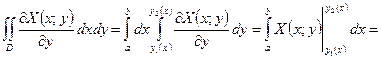
. (3)

Тогда

; .

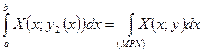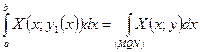Подставим эти выражения в формулу (3):

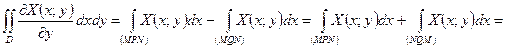
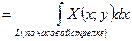. (4)

Аналогично,

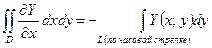(5)

Из равенств (4) и (5) следует:

.

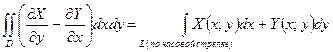Если обход L осуществляется против часовой стрелки, то

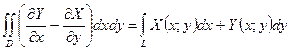. (6)

Формула (6) называется формулой Грина.

Пример: Применив формулу Грина, вычислить интеграл по контуру треугольника ABC с вершинами A(2;0), B(2;2), C(0;2).

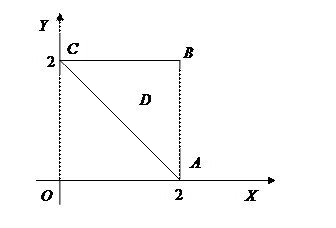
Так как 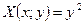, , 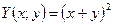получаем 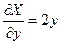, . Тогда

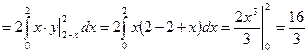
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.