
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Урок № 81 Тема: Иррациональные уравнения.
Урок № 81 Тема: Иррациональные уравнения.
Ход урока
1. Организационный момент.
2. Актуализация опорных знаний.





3. Изучение нового материала
Для решения иррациональных уравнений необходимо уметь выполнять с уравнениями простейшие преобразования, в том числе «избавляться» от корня. Что делать, если в одной из частей у нас имеется выражение под знаком корня? Всё просто:
Если корень квадратный, то обе части уравнения возводим в квадрат.
Если корень третьей степени, то обе части возводим в третью степень.
Здесь работает следующее свойство:
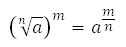
В случае, когда m = n, получаем что m делённое на n равно единице.
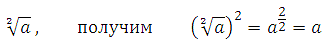 Например, возведём в квадрат выражение:
Например, возведём в квадрат выражение:
Если привести пример в числах:
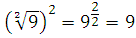
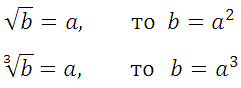 Даже без знания формул и свойств понятно, что если
Даже без знания формул и свойств понятно, что если
Ещё раз напоминаю, ОБЯЗАТЕЛЬНО делайте проверку после того, как нашли корни. Рассмотрим задания, которые входят в открытый банк заданий ЕГЭ.
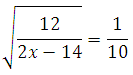
Пример 1. Найдите корень уравнения:
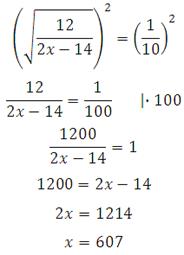
Для того, чтобы избавится от корня, возведём обе части уравнения в квадрат:
Сделайте проверку.
Ответ: 607
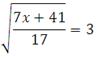 Пример 2.
Пример 2.
Найдите корень уравнения:
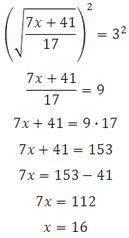 Возведём обе части уравнения в квадрат:
Возведём обе части уравнения в квадрат:
Сделайте проверку.
Ответ: 16
Пример 3.
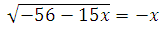
Найдите корень уравнения:
Если уравнение имеет более одного корня, укажите меньший из них.
Здесь необходимо отметить, что – х ≥ 0, то есть х ≤ 0, так как результат подкоренного выражения есть число неотрицательное. Это означает, что если при решении уравнения получим корни большие нуля, то они не будут являться решением, так как не попадают в область определения.
Возведём обе части уравнения в квадрат:
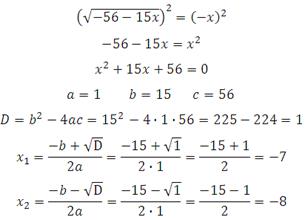 |
Сделайте проверку.
Оба корня удовлетворяют неравенству. Выберем меньший.
Меньший из них – 8.
Ответ: – 8
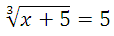 Пример 4.
Пример 4.
Найдите корень уравнения:
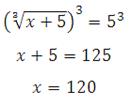
Возведём обе части уравнения в третью степень:
Сделайте проверку.
Ответ: 120
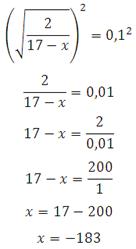
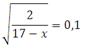 Пример 5.
Пример 5.
Решите уравнение:
Возводим в квадрат обе части, чтобы избавится от корня:
Ответ: –183
Пример 6.
 |
Приме 7.
 |
Самостоятельная работа. Проверь себя.
 |

 |


Домашняя работа
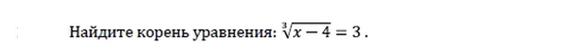 Уравнение 1.
Уравнение 1.


 Уравнение 2.
Уравнение 2.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|