Б класс. Алгебра и начала математического анализа.

11 - Б класс. Алгебра и начала математического анализа.

02.11.21

Тема урока: Свойства функции и ее график.

Посмотрите видео по ссылке: https://resh.edu.ru/subject/lesson/4920/main/200706/

Напомню, что все тригонометрические функции являются периодическими функциями. Функци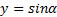и и 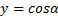повторяются через каждые 360° (или 2π радиан), поэтому 360° называется периодом этих функций (рис.1).

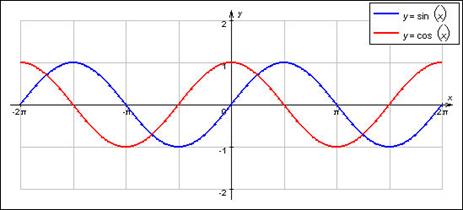
Рис. 1 – графики функци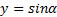й и .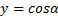

Функци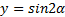и и 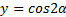повторяются через каждые 180° (или π радиан), поэтому 180° — это период для данных функций (рис. 2).

Рис. 2 – графики функци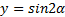й и .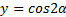

В общем случае если 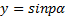и (где — константа), то период функции равен 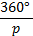(или 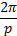радиан). Следовательно, если 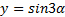, то период этой функции равен 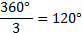, если 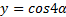, то период этой функции равен .

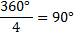Амплитудой называется максимальное значение синусоиды. Каждый из графиков 1-4 имеет амплитуду +1 (т.е. они колеблются между +1 и -1).

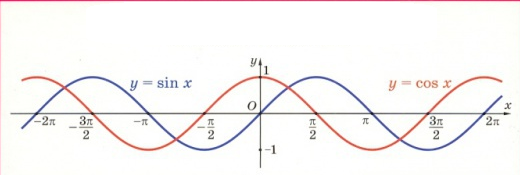
Рис. 3 – изображение амплитуды графиков 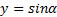и .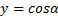

Однако, если 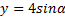, каждая из величин 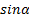умножается на 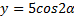4, таким образом, максимальная величина амплитуды — 4. Аналогично для амплитуда равна

5, а период— .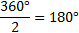

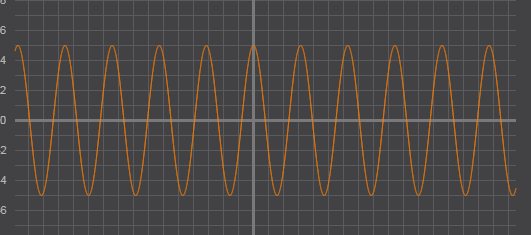
Рис. 4 – график функции .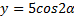

Свойства функции :

1. Область определения - множество R всех действительных чисел.

2. Множество значений - отрезок [−1;1].

3. Функция периодическая, Т=2π.

4. Функция - чётная

5. Функция принимает:

· значение, равное 0, при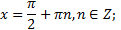

· наибольшее значение, равное 1, при

· наименьшее значение, равное −1, при ;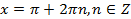

· положительные значения на интервале 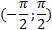и на интервалах, получаемых сдвигами этого интервала на ;

· отрицательные значения на интервале 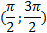и на интервалах, получаемых сдвигами этого интервала на .

1. Функция

· возрастает на отрезке [π;2π] и на отрезках, получаемых сдвигами этого отрезка на ;

· убывает на отрезке [0;π] и на отрезках, получаемых сдвигами этого отрезка на .

Интересно, что графиками тригонометрических функций –косинус и синус описываются многие процессы в нашей жизни. Например, работа сердца. Сделанная электрокардиограмма (ЭКГ) представляет собой график синусоиды, отражающую биоэлектрическую активность сердца. Или еще пример, электромагнитные волны к ним относятся: мобильные телефоны, беспроводная связь, радио, СВЧ-печи тоже распространяются по закону синуса или косинуса. Их существование было предсказано английским физиком Дж.Максвеллом в 1864 году.

Актуализация знаний

Напомню, что множество значений функции y=cosx принадлежит отрезку [–1;1], определена данная функция на всей числовой прямой и, следовательно, функция ограничена и график её расположен в полосе между прямыми y=–1 и y=1.

Так как функция периодическая с периодом 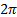, то достаточно построить её график на каком-нибудь промежутке длиной 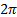, например на отрезке 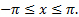Тогда на промежутках, полученных сдвигами выбранного отрезка на , график будет таким же.

Функция является чётной. Поэтому её график симметричен относительно оси Оу. Для построения графика на отрезке 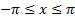достаточно построить для 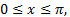а затем симметрично отразить его относительно оси Оу (рис. 5)

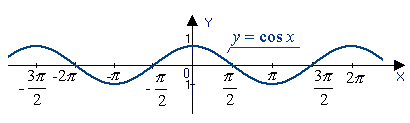
Рис. 5 – график функции .

Примеры и разборы решения задач запишите в тетради:

Пример 1. Найдем все корни уравнения 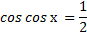, принадлежащие отрезку .

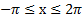Построим графики функци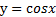й и (рис. 6)

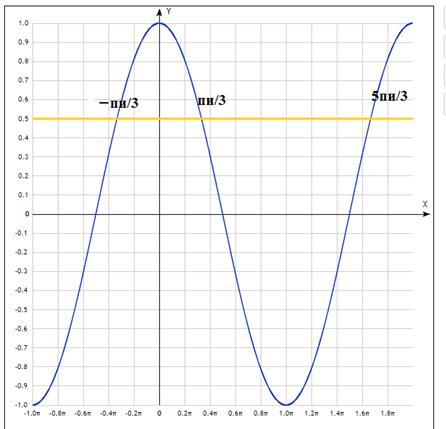
Рис. 6 – графики функци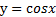й и .

Графики пересекаются в трёх точках, абсциссы которых являются корнями уравнения 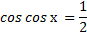. На отрезке от 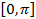корнем уравнения является число 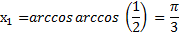. Из рисунка видно, что точки х₁ и х₂ симметричны относительно оси Оу, следовательно 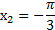. А .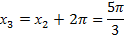

Пример 2.Найти все решения неравенства 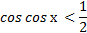, принадлежащие отрезку .

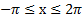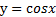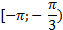Из рисунка 6 видно, что график функции лежит ниже графика функции на промежутках и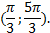

Ответ: , .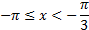

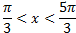Домашнее задание:Выполнить №712, №717(1, 3).