ОБРАТНАЯ СВЯЗЬ С УЧИТЕЛЕМ. Дополнительный материал

ОБРАТНАЯ СВЯЗЬ С УЧИТЕЛЕМ

Выполненную классную работу и домашнюю работу (скан или фото) для проверки отправить учителю на электронную почту:

rjdfktdf1957@mail.ru

или по Вайберу на номер 071 326 55 66

Время отправления: до 16.11.2021 до 16.00

Дополнительный материал

Датский астроном Тихо Браге, многие годы наблюдая за движением планет, накопил многочисленные данные, но не сумел их обработать. Это сделал его ученик Иоганн Кеплер. Используя идею Коперника о гелиоцентрической системе и результаты наблюдений Тихо Браге, Кеплер установил законы движения планет вокруг Солнца. Но Кеплер не сумел объяснить динамику движения. Почему планеты обращаются вокруг Солнца именно по таким законам? На этот вопрос сумел ответить Исаак Ньютон, использую законы движения, установленные Кеплером, и общие законы динамики.

Ньютон предположил, что ряд явлений, казалось бы, не имеющих ничего общего (падение тел на Землю, обращение планет вокруг Солнца, движение Луны вокруг Земли, приливы и отливы и т.д.), вызваны одной причиной. Проведя многочисленные расчеты, Ньютон пришел к выводу, что небесные тела притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.

Покажем, как Ньютон пришел к такому заключению. действием силы, обратно пропорционально массе тела. Но ускорение свободного падения не зависит от массы тела. Это возможно только в том случае, если сила, с которой Земля притягивает тело, изменяется пропорционально массе тела.

По третьему закону силы, с которыми взаимодействуют тела, равны. Если сила, действующая на одно тело, пропорциональна массе этого тела, то равная ей сила, действующая на второе тело, очевидно, пропорциональна массе второго тела. Но силы, действующие на оба тела, равны, следовательно, они пропорциональны массе и первого и второго тела.

Ньютон рассчитал отношение радиуса орбиты Луны к радиусу Земли. Отношение равнялось 60. А отношение ускорения свободного падения на Земле к центростремительному ускорению, с которым обращается вокруг Земли Луна, равнялось 3600. Следовательно, ускорение обратно пропорционально квадрату расстояния между телами.

Но по второму закону Ньютона сила и ускорение связаны прямой зависимостью, следовательно, сила обратно пропорциональна квадрату расстояния между телами.

Исаак Ньютон открыл этот закон в возрасте 23 лет, но 9 лет не публиковал, так как неверные данные о расстоянии между Землей и Луной не подтверждали его идею. И только когда было уточнено это расстояние, Ньютон в 1667 г. опубликовал закон всемирного тяготения.

Сила гравитационного взаимодействия двух тел (материальных точек) с массами m, и m₂ равна:

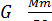
где G - гравитационная постоянная, R - расстояние между телами. Гравитационная постоянная численно равна модулю силы тяготения, действующей на тело массой 1 кг со стороны другого тела такой же массы при расстоянии между телами равном 1 м.

Впервые гравитационная постоянная была измерена английским физиком Г. Кавендишем в 1788 г. с помощью прибора, называемого крутильными весами. Г. Кавендиш закрепил два маленьких свинцовых шара (диаметром 5 см и массой 775 г каждый) на противоположных концах двухметрового стержня. Стержень был подвешен на тонкой проволоке. Два больших свинцовых шара (20 см диаметром и массой 45,5 кг) близко подводились к маленьким. Силы притяжения со стороны больших шаров заставляли маленькие перемещаться, при этом проволока закручивалась. Степень закручивания была мерой силы, действующей между шарами. Эксперимент показал, что гравитационная по- тоянная G = 6,66 • 10~" Н м^кг².

Пределы применимости закона

Закон всемирного тяготения применим только для материальных точек, т.е. для тел, размеры которых значительно меньше, чем расстояния между ними; тел, имеющих форму шара; для шара большого радиуса, взаимодействующего с телами, размеры которых значительно меньше размеров шара.

Но закон неприменим, например, для взаимодействия бесконечного стержня и шара. В этом случае сила тяготения обратно пропорциональна только расстоянию, а не квадрату расстояния. А сила притяжения между телом и бесконечной плоскостью вообще от расстояния не зависит.

Сила тяжести

Частным случаем гравитационных сил является сила притяжения тел к Земле. Эту силу называют силой тяжести.

В этом случае закон всемирного тяготения имеет вид:

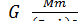
где т - масса тела [кг],

М - масса Земли [кг],

R - радиус Земли [м],

h - высота над поверхностью [м].

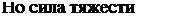F=mg, отсюда mg = G_г-, а ускорение свободного

падения g=9,81м/с²

Ускорение свободного падения зависит

♦ от высоты над поверхностью Земли;

♦ от широты местности (Земля - неинерциальная система отсчета);

♦ от плотности пород земной коры;

♦ от формы Земли (приплюснута у полюсов).

В приведенной выше формуле для# последние три зависимости не учитываются. При этом еще раз подчеркнем, что ускорение свободного падения не зависит от массы тела.

Применение закона при открытии новых планет

Когда была открыта планета Уран, на основе закона всемирного тяготения рассчитали ее орбиту. Но истинная орбита планеты не совпала с расчетной. Предположили, что возмущение орбиты вызвало наличием еще одной планеты, находящейся за Ураном, которая своей силой тяготения изменяет его орбиту. Чтобы найти новую планету, необходимо было решить систему из 12 дифференциальных уравнений с 10 неизвестными. Эту задачу выполнил английский студент Адамс; решение он отправил в Английскую академию наук. Но там на его работу не обратили внимания. А французский математик Леверье, решив задачу, послал результат итальянскому астроному Галле. И тот, в первый же вечер наведя свою трубу в указанную точку, обнаружил новую планету. Ей дали название Нептун. Подобным же образом в 30-е годы двадцатого века была открыта и 9-я планета Солнечной системы - Плутон.

На вопрос о том, какова природа сил тяготения, Ньютон отвечал: «Не знаю, а гипотез измышлять не желаю».

⇐ Предыдущая 12