Рис. 3.49. Деление окружности на три части с построением вписанного треугольника

Тема:Разметка.

Деление окружности на равные части и построение многоугольников.

Деление окружности на три равные части с построением вписанного треугольника (рис. 3.49).

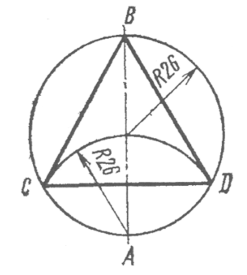
Рис. 3.49. Деление окружности на три части с построением вписанного треугольника

1. В центре размечаемой плоскости с помощью циркуля проводим окружность требуемого радиуса, например R = 26 мм.

2. Через центр окружности по линейке проводим прямую риску с пересечением окружности в точках А и В.

3. Опорную ножку циркуля устанавливаем в точку А и при растворе циркуля, равном радиусу проведенной окружности, делаем на окружности две метки-засечки (точки С и D), где длина дуги между ними будет равна одной трети длины окружности.

4. Соединив точки прямыми рисками СД СВ и BD, получим вписанный равносторонний треугольник.

5. Правильность построения проверяем циркулем, устанавливая раствор циркуля равным одной из сторон треугольника и этим же размером определяя равенство остальных сторон треугольника.

Деление окружности на четыре равные части с построением вписанного квадрата, рис. 3.50.

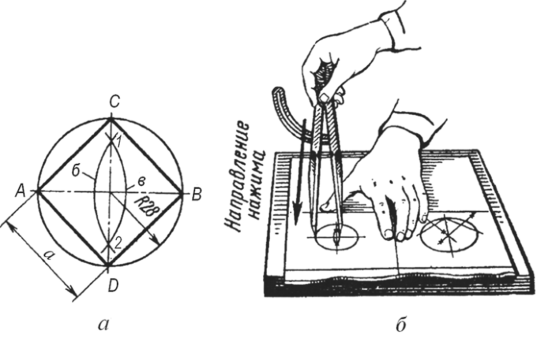
Рис. 3.50. Деление окружности на четыре части с построением вписанного квадрата(а)и прием разметки квадрата (6)

1. В центре размечаемой плоскости циркулем проводим окружность требуемого радиуса, например R= 28 мм.

2. Через центр окружности по линейке проводим прямую риску что бы она пересекала окружности в двух точках А и В и разделяла ее на две равные части.

3. Опорную ножку циркуля устанавливаем в точку А и, раздвинув циркуль на расстояние несколько большее, чем половина отрезка АВ, проводим дугу в.

4. Опорную ножку циркуля переносим в точку В и, не изменяя раствора циркуля, проводим дугу б так, чтобы она пересекла первую выполненную дугу в точках 7 и 2.

5. Через точки 7 и 2 проводим риску, которая образует на окружности точки С и D.

6. Соединив точки AD, DB, ВС и СА прямыми рисками, получим квадрат, вписанный в окружность.

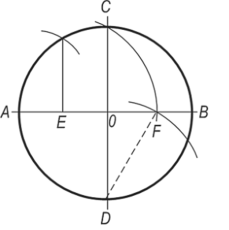
Деление окружности на пять равных частей (рис. 3.51). На данной окружности проводим два взаимно перпендикулярных диаметра, пересекающие окружность в точках А и В, С и D. Радиус ОА делим пополам и из полученной точки Е описываем дугу радиусом ЕС до пересечения в точке F на радиусе О В. После этого соединяем прямой точки D и F. Откладывая длину прямой DF по окружности, разделим ее на пять равных частей.

Деление окружности на шесть равных частей с построением вписанного шестиугольника, рис. 3.52.

12 Следующая ⇒