Критерий факторизации.

4.2. Критерий факторизации.

Необходимость вычислять условное распределение 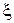(или распределение 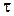), чтобы потом определить условное распределение делением 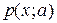на 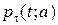, является весьма неудобным способом определения достаточности. Простой способ дает теорема, называемая критерием факторизации.

Теорема. Статистика T(ξ) достаточна для а тогда и только тогда, когда справедлива факторизация (представление):

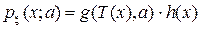Существенным в этой записи является то, что

множитель, зависящий от параметра, от x зависит только через 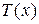, (напомним: 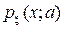понимается как плотность или вероятность).

Докажем утверждение для дискретного случая.

Достаточность.

Пусть 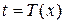(иначе выписанная ниже вероятность равна 0). Рассмотрим условную вероятность:

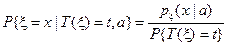
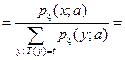
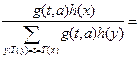
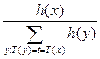Полученное выражение не зависит от а.

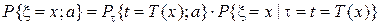Необходимость.

Пусть 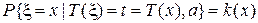не зависит от а. Тогда в силу (1)

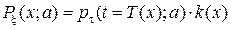то есть справедлива факторизация (2).

Замечание. Пусть 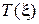— достаточная статистика.

Любая функция 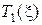, по которой можно получить достаточную 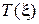, является тоже достаточной. Другими словами,

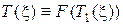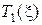если , то достаточна.

Этот факт тривиально следует из критерия факторизации:

= .

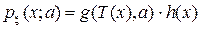
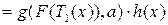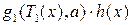В частности, есл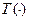и и связаны взаимооднозначно, то 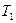— достаточна.

Пример 1. Пусть 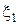, ξ₂ … 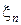— n независимых наблюдений над случайной величиной, распределенной по закону Пуассона, другими словами, 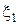, ξ₂… 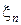— выборка из совокупности, распределенной по закону Пуассона. Распределение выборки имеет вид:

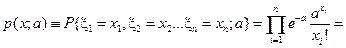
Видим, что множитель, зависящий от параметра а, т.е. 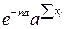, от x зависит только через 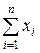.По критерию факторизации 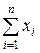является достаточной статистикой.

Пример 2. Пусть случайное событие А с неизвестной вероятностью q испытывается независимо n раз. Пусть ξ_i - результат 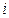-го испытания — случайная величина (i = 1, 2…n), распределенная следующим образом:

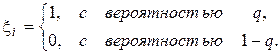
Пусть 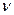— число наступлений события А в серии из n испытаний. Выпишем распределение вероятностей для выборки 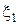, ξ₂… 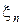, принимая во внимание, что любая из случайных величин 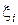может принимать лишь два значения (x_i = 0 или x_i = 1):

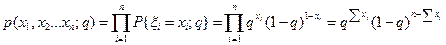Из этого выражения следует, что 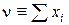является достаточной статистикой.

Пример 3. Пусть 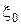— случайная величина, распределенная по равномерному закону на отрезке 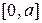, 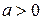. Плотность распределения (для ):

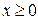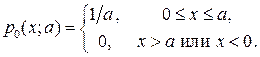
Пусть ξ₁, ξ₂…ξ_n есть n независимых наблюдений над ξ₀. Плотность распределения выборки:

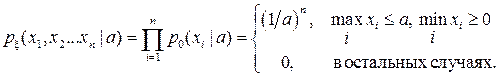[МА1]

Если ввести функцию 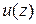— индикатор неотрицательности аргумента z, —определив ее так:

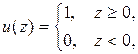
то плотность распределения выборки запишется в виде:

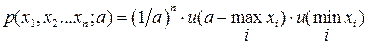[МА2] ,

откуда по критерию факторизации следует, что 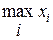является достаточной статистикой.

Пример 4. Пусть ξ₁, ξ₂…ξ_n — выборка из совокупности, распределенной по нормальному закону с параметрами m и 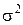(роль параметра а в критерии факторизации играет здесь двумерный параметр ).

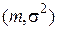Плотность распределения выборки имеет вид:

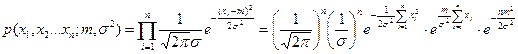Из этого выражения по критерию факторизации следует, что двумерная статистика 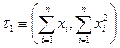является достаточной для 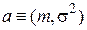, так же как и двумерная статистика

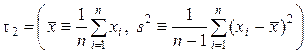связанная с τ₁ взаимно-однозначно и имеющая своими компонентами несмещенные оценк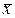и и 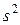для математического ожидания m и дисперсии 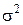. Поэтому любые статистические задачи, связанные с нормальным распределением, можно решать, опираясь на оценк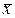и и .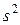

[МА1]Поправить в скобках (х₁, х₂…х_n)

[МА2]Поправить в скобках (х₁, х₂…х_n)

⇐ Предыдущая 12