
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: 1. Площадь полной поверхности призмы. Решение задач.
Тема: 1. Площадь полной поверхности призмы. Решение задач.
Дата: 25.10.2021 г.
Группа: МОЦИ-264
Студенты должны знать: понятие призмы, виды призм, понятие площади поверхности призмы, формулы для вычисления площади полной и боковой поверхности прямой призмы.
Студенты должны уметь:применять в задачах понятия призмы, площади поверхности призмы.
1. Проверка домашнего задания


 Задача №231
Задача №231
2. Актуализация опорных знаний
Подготовка к проверочной самостоятельной работе.
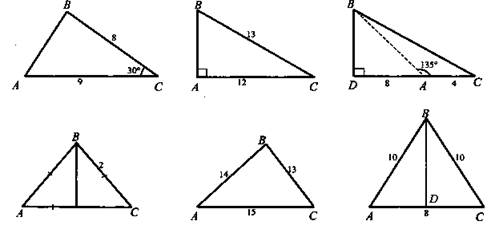 1. Устное решение задач планиметрии по готовым чертежам.
1. Устное решение задач планиметрии по готовым чертежам.
Найти площадь ΔАВС.
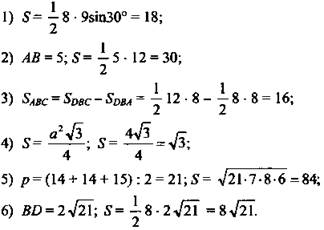
2. Письменное решение планиметрической задачи, краткий ход решения ученик записываете в тетради.
 Решение:
Решение:
1) КВ = х; ВМ = х; АМ = 13 - х; АL = 13 - х.
2) КС = СК = 2.
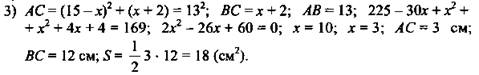
(Ответ: SABC = 18 см2.)
3. Применение знаний в стандартной ситуации
Задача. Основанием прямой призмы является прямоугольный треугольник, гипотенуза которого равна m, а острый угол равен 60°. Через катет, противоположный этому углу, и противоположную этому катету вершину другого основания проведено сечение, составляющее угол 45° с плоскостью основания.
1. Докажите, что ΔА1СВ прямоугольный.
2. Укажите различные способы вычисления площадей основания и сечения призмы.
3. Вычислите площадь основания призмы.
4. Вычислите площадь боковой поверхности призмы.
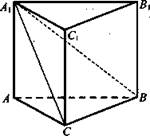 Решение:
Решение:
1) АС ⊥ СВ; AA1 ⊥ CB1, значит, АС ⊥ СВ; ΔА1СВ - прямоугольный.
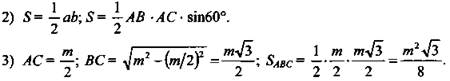
4) ΔАА1С - равнобедренный и прямоугольный, 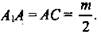
5) 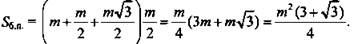 (Ответ:
(Ответ: 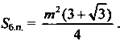 )
)
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|