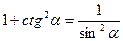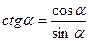- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическая работа №24. Теоретический материал. Знаки тригонометрических функций
Практическая работа №24
Тема: Выражение одних тригонометрических функций через другие
Цель работы: Научиться выводить формулы, позволяющие выражать значения одних тригонометрических функций через другие
Количество часов на выполнение практического задания – 2
Методические указания по выполнению работы:
Перед выполнением работы необходимо ознакомиться с теоретическим материалом по теме и ответить на контрольные вопросы. Номера строк из таблицы соответствуют списочным номерам студентов в журнале.
Во время выполнения работы студент может пользоваться своим конспектом, а также учебной литературой и справочным материалом.
Задание №1. Повторить теоретический материал по теме и письменно ответить на контрольные вопросы:
Теоретический материал
Основные тригонометрические тождества:
| 1. | sin2α + cos2α = 1 |
| 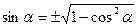
|
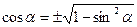
| |||
| 2. | tg α *ctg α = 1 |
| 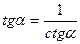
|
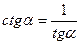
| |||
| 3. |
|
| 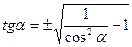
|
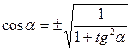
| |||
| 4. |
|
| 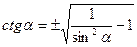
|
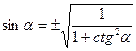
| |||
| 5. |
|
| 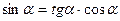
|
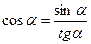
| |||
| 6. |
|
| 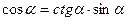
|
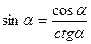
|
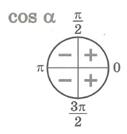
Знаки тригонометрических функций
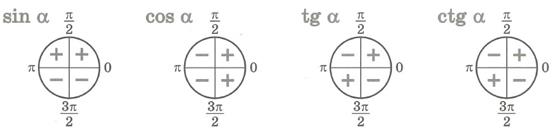
Образцы решений:
Задание №1.Найти cos α, если 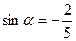 и
и 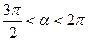 .
.
Дано:
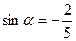
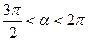
| Решение:
sin2α + cos2α = 1 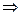 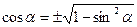
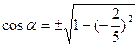
|
| Найти: cos α | 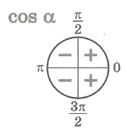 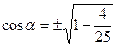
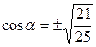 Так как
Так как 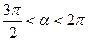 (IV четверть), то (IV четверть), то
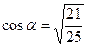 Ответ:
Ответ: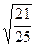 . .
|
Задание №2.Найти sin α , если 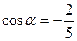 и
и 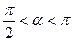 .
.
Дано:
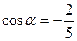
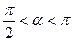
| Решение:
sin2α + cos2α = 1 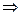 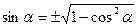
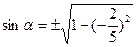
|
| Найти: sin α | 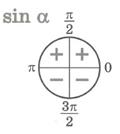 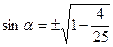
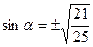 Так как
Так как 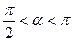 (II четверть), то (II четверть), то
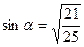 Ответ:
Ответ: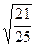 . .
|
Задание №3.По заданному значению функции найдите значения остальных тригонометрических функций
Дано:
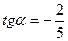
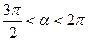
| Решение:
1). 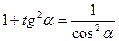 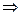 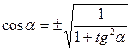
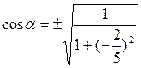
|
| Найти: cos α, sin α, ctg α | 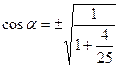
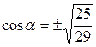
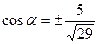 Так как
Так как 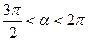 (IV четверть), то (IV четверть), то
 2).
2). 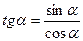 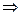 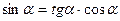
 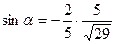
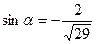 3).tg α *ctg α = 1
3).tg α *ctg α = 1 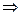 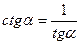
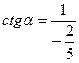
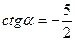 Ответ:
Ответ: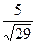 ; ; 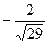 ; ; 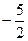 . .
|
Контрольные вопросы:
1. Дайте определения основных тригонометрических функций.
2. Определите знак выражения: sin 2200*cos 4300*tg(-890).
3. Запишите формулы, связывающие значения тригонометрических функций одного аргумента.
Практическая часть. Решить задачи:
| № варианта | Найти cosα, если … | Найти sinα, если … | По заданному значению функции найдите значения остальных тригонометрических функций |
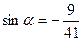 и и 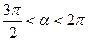
| 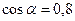 и и 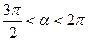 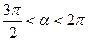
| 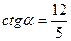 и и 
| |
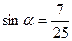 и и 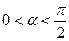
|  и и 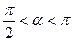
| 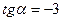 и и 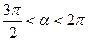
| |
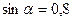 и и 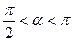
| 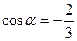 и и 
| 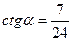 и и 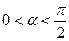
| |
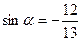 и и 
| 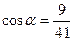 и и 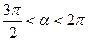
| 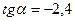 и и 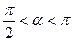
| |
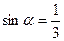 и и 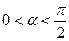
|  и и 
| 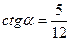 и и 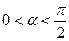
| |
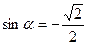 и и 
| 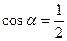 и и 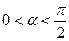
| 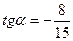 и и 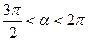
| |
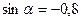 и и 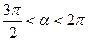
| 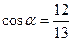 и и 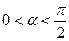
| 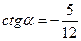 и и 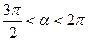
| |
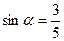 и и 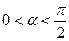
| 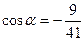 и и 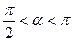
| 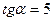 и и 
| |
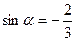 и и 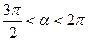
| 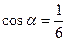 и и 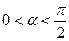
| 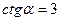 и и 
| |
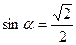 и и 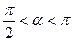
| 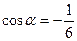 и и 
| 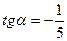 и и 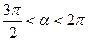
|
Сделать вывод о проделанной работе.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|