Задания школьного этапа Республиканской олимпиады школьников по математике 2021-2022 уч.г.

Задания школьного этапа Республиканской олимпиады школьников по математике 2021-2022 уч.г.

6 класс

1.Вычислите: .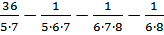

2. «Ну, погоди!» - закричал Волк, заметив, в 30 метрах Зайца, и бросился за ним. На каком расстоянии они будут через 5 минут, если Заяц пробегает 500 метров в минуту, а Волк – 450?

3.Из 210 бордовых, 126 белых, 294 красных роз собрали букеты, причём в каждом букете количество роз одного цвета поровну.

Какое наибольшее количество букетов сделали из этих роз и сколько роз каждого цвета в одном букете?

4. К числу 2018слева и справа припишите по одной цифре

так, чтобы полученное число делилось на 45. Запишите все возможные варианты.

5. Разрежьте фигуру на рисунке по клеточкам на 6 равных частей. Части считаются равными, если их можно наложить друг на друга так, чтобы они полностью совпали.

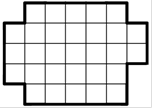
7 класс

1. Два велосипедиста выехали одновременно из двух городов навстречу друг другу. Когда они встретились, то выяснилось, что один из них проехал 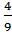всего пути и еще 12 км, а второй – 50% того, что проехал первый. Найдите расстояние между городами.

2. Задумали некоторое число. Если из него вычесть 7 и полученную разность умножить на 7, получится то же самое, как если бы из него вычли 11 и полученную разность умножили на 11. Какое число задумали?

3. У Карлсона было две полные банки варенья. Одна из банок в три раза больше другой. Когда в маленькой банке осталось 2 литра варенья, а в большой – 13 л, Карлсон долил доверху маленькую банку из большой. В результате в большой банке осталась половина первоначального количества варенья. Найдите объём банок с вареньем.

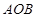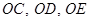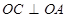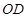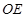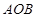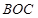4. Внутри тупого угла провели лучи так, что , а и – биссектрисы углов и соответственно. Найти величину угла .

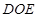5. На доске записано число 61. Каждую минуту число стирают с доски и записывают на это место произведение его цифр, увеличенное на 13. То есть, через одну минуту на доске будет записано 19 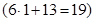. Какое число можно будет прочитать на доске через час?

8 класс

1. Сухие грибы по массе содержат 12% воды, а свежие - 90%. Сколько получится сухих грибов из 22 кг свежих грибов?

2. Три фирмы 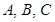решили совместно построить дорогу длиной 16 км, договорившись финансировать этот проект поровну. В итоге, 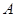построила 6 км дороги, 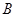построила 10 км, а 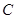внесла свою долю деньгами – 16 миллионов рублей. Каким образом фирмы 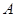и 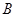должны разделить эти деньги между собой?

3. Разность квадратов двух чисел равна 6, а если уменьшить каждое из этих чисел на 2, то разность их квадратов станет равна 18. Чему равна сумма этих чисел?

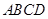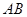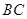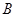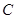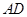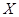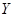4. В прямоугольнике сторона равна 6 см, сторона равна 11 см. Из вершин и проведены биссектрисы углов, пересекающие сторону в точках и соответственно. Найдите длину отрезка .

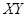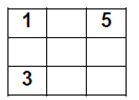
5. В трёх клетках таблицы 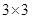стоят числа (см. рисунок). Требуется заполнить числами остальные клетки так, чтобы во всех строках, столбцах и главных диагоналях суммы чисел оказались равными.

9 класс

1. Графики функци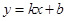й и 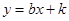пересекаются. Найдите абсциссу точки пересечения.

2. Известно, что 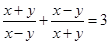. Найдите значение выражения .

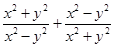3. Пусть 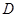- дискриминант приведенного квадратного трёхчлена 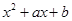. Найдите корни трёхчлена, если известно, что они различны и один из них равен , а другой равен .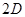

4. В равнобедренном треугольнике 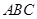угол равен 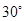, 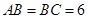см. Проведены высота 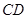треугольника 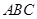и высота 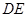треугольника 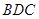. Найдите длину .

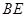5. Квадрат 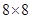разрезали на квадраты 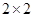и прямоугольники 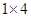. При этом общая длина распилов оказалась равна 54. Сколько фигурок каждого вида получилось?

10 класс

1. На доске записано несколько последовательных натуральных чисел. Ровно 52% из них – чётные. Сколько чётных чисел записано на доске?

2. Найдите наименьшее целое решение неравенства: .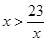

3. Найти наименьшее возможное шестизначное число вида 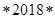, в котором вместо звездочек стоят цифры такие, что это число делится на 36.

4. В треугольнике ABC известно, что AB = BC, AC = 10 см. Из середины D стороны AB проведён перпендикуляр DE к стороне AB до пересечения со стороной BC в точке E. Периметр треугольника ABC равен 40 см. Найдите периметр треугольника AEC.

5. Найдите коэффициенты 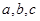квадратичной функции 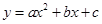, зная, что этот график пересекает ось 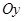в точке 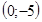и имеет ровно одну общую точку 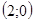с осью .

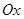11 класс

1. Числовая функция 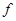такова, что для любых 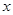и 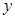выполняется равенство: 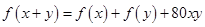. Найдите 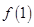, если .

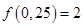2. Известно, что 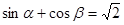и 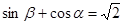. Чему равно значение 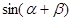и значение ?

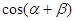3. Прямоугольный участок выложен квадратными плитками. Если и длину, и ширину участка увеличить на 7 плиток каждую, то общее число плиток станет в 3,5 раза больше числа плиток, которые будут лежать вдоль периметра участка. Сколько сейчас плиток на участке?

4. Боковые стороны трапеции равны меньшему основанию, а диагонали – большему. Найдите углы трапеции.

5. Найти все трёхзначные числа, которые в 5 раз больше произведения своих цифр.