Точки разрыва функции и их классификация.

Непрерывность функции.

Непрерывные функции, точки разрыва и их классификация.

Определение:

Функция у = f(x) называется непрерывной в точке х₀, если:

· функция определена в точке x₀ и в некоторой ее окрестности, содержащей эту точку;

· функция имеет предел при х → x₀;

· предел функции при х → x₀ равен значению функции в точке x₀:
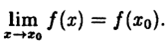(1)

Если в точке x₀ функция непрерывна, то точка x₀ называется точкой непрерывности функции.

1 Пример:

Исследовать на непрерывность функцию 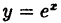в точке х = 1.

Решение:

Чтобы доказать, что функция 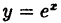непрерывна в точке х = 1, необходимо проверить выполнение трех следующих условий (определение непрерывности):

· функция определена в точке х = 1 ⇒ f(1) = e;

· существует ;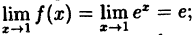

· этот предел равен значению функции в точке х = 1 :

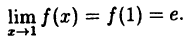
Таким образом, доказано, что функция 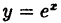непрерывна в точке х = 1.

Введем понятие непрерывности функции в точке х₀ справа и слева.
Если, существует 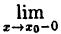f(x) = f(x₀), то функция называется непрерывной в точке x₀ слева. Аналогично определяется непрерывность функции справа.

Так как ∆x = x-x₀, a ∆y = f(x)-(x₀), то условие (1) равносильно следующему:

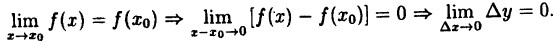
Точки разрыва функции и их классификация.

Определение:

Точка х₀ называется точкой разрыва функции у = f(x), если она принадлежит области определения функции или ее границе и не является точкой непрерывности.

Так, например, функция 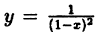(рис. 89) терпит разрыв при х = 1. Эта функция не определена в точке х = 1, и не существует предела функции в этой точке.

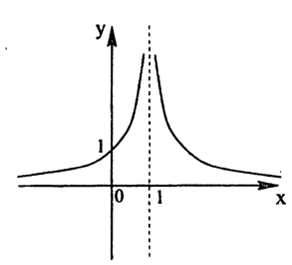Рис. 1. График функции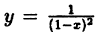

Определение:

Точка разрыва x₀ функции у = f(x) называется точкой устранимого разрыва, если существуют оба односторонних предела в точке x₀ и они равны, А.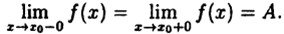

2 Пример:

Исследовать на непрерывность функцию

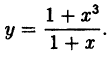
Решение:

В точке x=-1 функция не определена, так как, выполнив подстановку, получаем неопределенность 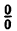. В других точках дробь можно сократить на (1 + х), так как в них 1 + х ≠ 0. Легко видеть, что односторонние пределы слева и справа в точке х = — 1 равны между собой и их можно вычислить:

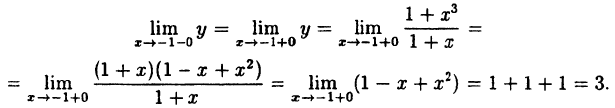
Таким образом, при x = -1 данная функция имеет устранимый разрыв.
Он будет устранен, если положить, что при x = -1 ⇒ у = 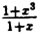= 3.

Определение:

Если в точке x₀ односторонние пределы слева и справа существуют, но не равны, точка x₀ называется точкой разрыва I рода.

Определение:

Точки разрыва, не являющиеся точками разрыва I рода, называются точками разрыва II рода.

В точках разрыва II рода не существует хотя бы один из односторонних пределов. Функция 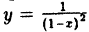, представленная на рис. 1, не имеет ни левого, ни правого конечного предела в точке х = 1. Следовательно, для данной функции x = 1 является точкой разрыва II рода.

3 Пример:

Показать, что функция у = 4x² непрерывна в точке х = 2.

Решение:

Для этого необходимо показать, что в точке х = 2 выполняется все три условия непрерывности функции:

1) функция у = 4х² определена в точке х = 2 ⇒ f(2) = 16;
2) существует 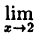f(x) = 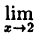4x²= 16;
3) этот предел равен значению функции в точке х = 2

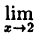f(x) = f(2) = 16.

4 Пример:

Исследовать на непрерывность функцию

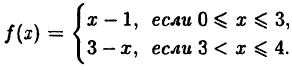
Решение:

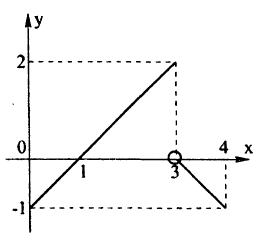Рис.2. График функции примера

Эта функция (рис. 2) определена во всех точках сегмента [0,4] и ее значение при х = 3 ⇒ у = 2. Функция терпит разрыв, так как она не имеет предела при х → 3 :

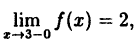
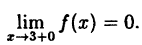
Следовательно, точка х = 3, точка разрыва I рода. При этом в граничных точках исследуемого сегмента [0,4], функция f(x) непрерывна справа (х = 0) и непрерывна слева (х = 4).

5 Пример:

Исследовать на непрерывность функцию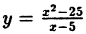

Решение:

В точке х = 5 функция не определена, т.к., выполнив подстановку, получаем неопределенность вида 0/0. Легко доказать, что

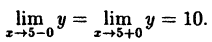
Следовательно, точка х = 5 точка устранимого разрыва.

6 Пример:

Исследовать на непрерывность функцию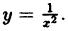

Решение:

В точке х = 0 функция (рис. 2) терпит разрыв, так как она не определена в этой точке. Пределы функции слева и справа от точки х = 0 равны ∞. Следовательно, точка х = 0 для данной функции является точкой разрыва II рода.

Определение:

Если функция непрерывна в каждой точке некоторого промежутка, то ее называют непрерывной на данном промежутке.