
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Примеры и разбор решения заданий
Лекция 7.«Способы решения показательных неравенств»
Показательным называется неравенство, в котором переменная входит только в показатели степеней, при постоянном основании.
Неравенства вида 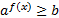 ,
, 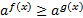 называются простейшими показательными неравенствами.
называются простейшими показательными неравенствами.
В самом простом случае неравенство принимает вид: 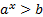 .
.
Очевидно, что знак неравенства может быть любым (<, >, 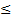 ,
,  ).
).
Множество решения неравенства будет зависеть и от знака неравенства, и от основания степени, и от значения b.
Так как множество значений показательной функции 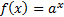 – множество положительных чисел, то при
– множество положительных чисел, то при  неравенства:
неравенства: 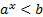 и
и  решений не имеют, независимо от значения основания а. В то же время множеством решения неравенств
решений не имеют, независимо от значения основания а. В то же время множеством решения неравенств 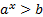 и
и 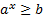 является все множество действительных чисел, независимо от значения основания а.
является все множество действительных чисел, независимо от значения основания а.
Теперь рассмотрим случай b>0, a>1.
В том случае, когда основание степени a>1, то при переходе от исходного неравенства к неравенству с показателями знак неравенства не изменяется.
Теперь рассмотрим случай b>0, 0<a<1.
В том случае, когда основание степени 0<a<1, то при переходе от исходного неравенства к неравенству с показателями знак неравенства изменяется на противоположный.
Для того чтобы решить простейшее показательное неравенство 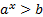 , нужно число b представить в виде степени числа a.
, нужно число b представить в виде степени числа a.
Рассмотрим пример: 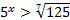 .
.
Представим 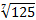 в виде степени числа 5:
в виде степени числа 5: 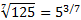 .
.
Теперь перепишем данное неравенство в виде:  .
.
Так как основание степени больше 1, то при переходе к показателям знак неравенства сохраняется, поэтому x>3/7.
Ответ: x>3/7.
Рассмотрим еще один пример: 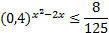 .
.
Перепишем его в виде
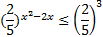 .
.
Так как основание степени меньше 1, то при переходе к показателям знак неравенства изменяется на противоположный:
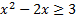 ,
,
 ,
,
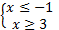 .
.
Ответ: 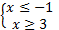 .
.
Теперь перейдем к решению более сложных показательных неравенств.
1) Рассмотрим пример: 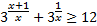 .
.
Преобразуем показатель первого слагаемого: 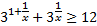 .
.
Теперь в левой части вынесем за скобку общий множитель:  .
.
Разделим обе части неравенства на 4: 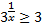 . Получили простейшее показательное неравенство. Так как основание степени больше 1, то при переходе к показателям знак неравенства сохраняется, получаем:
. Получили простейшее показательное неравенство. Так как основание степени больше 1, то при переходе к показателям знак неравенства сохраняется, получаем: 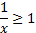 . Решение этого неравенства является полуинтервал (0; 1].
. Решение этого неравенства является полуинтервал (0; 1].
Ответ: (0; 1].
2) Рассмотрим еще один пример: 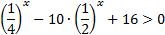 .
.
Заметим, что 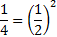 , поэтому введем новую переменную
, поэтому введем новую переменную  . Получим вспомогательное неравенство:
. Получим вспомогательное неравенство: 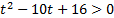 .
.
Решим его:
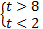 .
.
Вернемся к исходной переменной:
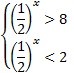 ,
, 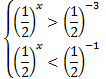 .
.
Так как основание степени меньше 1, то при переходе к показателям знак неравенства изменится на противоположный:
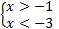 .
.
Ответ: 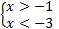 .
.
3) Рассмотрим еще одной показательное неравенство, которое решается методом замены переменной.
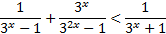 .
.
Видим, что неравенство зависит от выражения 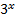 , поэтому введем новую переменную
, поэтому введем новую переменную 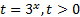 и запишем вспомогательное неравенство:
и запишем вспомогательное неравенство: 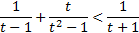 .
.
Преобразуем полученное неравенство к виду: F(t)<0.
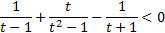 , приведем левую часть к общему знаменателю:
, приведем левую часть к общему знаменателю:
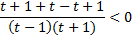 ,
, 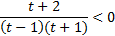 . Так как
. Так как 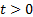 , то
, то 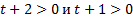 , поэтому решение полученного неравенства сводится к:
, поэтому решение полученного неравенства сводится к: 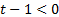 , то есть
, то есть 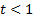 .
.
Вернемся к исходной переменной: 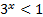 , то есть x<0.
, то есть x<0.
Ответ: 
Примеры и разбор решения заданий
1. 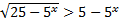 .
.
Решение:
Введем новую переменную 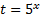 .
.
Запишем вспомогательное неравенство: 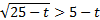 .
.
1) Если 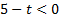 , то решением неравенства является любое значение t, которое удовлетворяет области определения:
, то решением неравенства является любое значение t, которое удовлетворяет области определения: 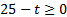 .
.
Решив систему:  , получаем:
, получаем:  .
.
2) Если 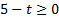 (
(  ), возведем обе части неравенства в квадрат:
), возведем обе части неравенства в квадрат:
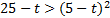 .
.
Решим его:  ,
,
 ,
,
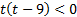 ,
,
0<t<9.
Учитывая условие  , получаем:
, получаем: 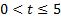 .
.
Таким образом, объединяя первый и второй случай, получаем решение иррационального вспомогательного неравенства:
 .
.
Вернемся к исходной переменной:
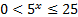 . Так как
. Так как  всегда, то получаем:
всегда, то получаем: 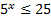 .
.
Учитывая, что основание степени больше 1, получаем:

Ответ: 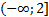 .
.
2. (x^2+x+1)^((x+5)/(x+2)) 
Решение:
Используем метод рационализации и перепишем неравенство в виде:
 ,
,
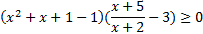 .
.
Получили неравенство: 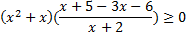 .
.
Упростим его и решим методом интервалов:
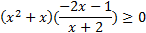 ,
,
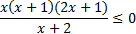 .
.

Запишем ответ: 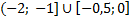 .
.
Ответ: 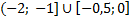 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|