Среднее арифметическое.. Среднее взвешенное.

Лекция №4. Вычисление среднего значения.

1. Среднее арифметическое.

2. Среднее взвешенное.

3. Медиана.

4. Мода.

1. Среднее арифметическое.

Среднее арифметическое вычисляется путем сложения всех значений набора данных и деления полученной суммы на количество наблюдений. Математическая формула для вычисления среднего несколько варьируется в зависимости от того, вычисляете ли вы среднее по выборке или среднее по совокупности (математическое ожидание). Вычисление выборочного среднего выполняется по следующей формуле:

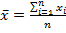, где: – среднее по выборке, 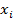– значение выборки ( 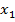- значение первого аргумента выборки, 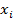– значение второго аргумента выборки и так далее),

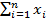=сумма всех значений данной выборки,

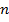– количество значений данных выборки.

Выражение 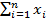означает сумму x при i = от 1 до n. Если, к примеру, наша выборка содержит значения 5, 8 и 2, тогда 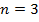, , 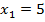, , 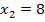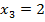в результате чего получаем выражение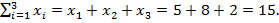

Пример. Набор данных, представляющий собой количество часов, проводимых за видеоиграми в семье каждую неделю: 3 7 4 9 5 4 6 17 4 7.

Поскольку эти данные представляют собой выборку, мы можем вычислить среднее по выборке:

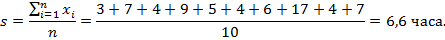
2. Среднее взвешенное.

При расчете среднего количества часов в предыдущем примере каждому значению присваивается один и тот же вес. Взвешенное среднее позволяет приписывать некоторым значениям больший вес, а другим – меньший.

Пример. Ваша оценка по статистике в этом семестре будет складываться из экзаменационной оценки, оценки за домашнюю работу и научный проект. Каждому компоненту итоговой оценки присваивается вес в соответствии со следующей таблицей:

Тип	Результат	Вес (процент)
Экзамен
Проект
Домашнее задание

Мы можем рассчитать вашу итоговую оценку, воспользовавшись следующей формулой расчета взвешенного среднего. Обратите внимание, что здесь мы делим на сумму присвоенных весов, а не количество значений данных:

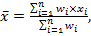где: 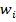= вес каждого значения данных 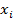, 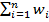= сумма весов.

Выражение 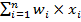означает сумму произведени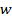й и 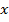. Каждая пара сначала перемножается, а затем результат суммируется.

Предыдущее уравнение можно представить в виде следующей таблицы, чтобы вам была понятна процедура:

Тип	Результат	Вес	Вес × Результат (w×x)
Экзамен		0,50	47,0
Проект		0,35	31,2
Домашнее задание		0,15	12,4

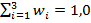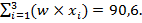
Тот же результат может быть получен путем вставки чисел непосредственно в формулу расчета взвешенного среднего:

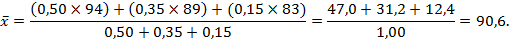
3. Медиана.

Медианой называется такое значение набора данных, по отношению к которому половина наблюдений имеют большее значение, а половина – меньшее. Для определения медианы необходимо расположить значения данных по возрастанию и найти центральное значение.

Вернемся к примеру с видеоиграми и выстроим наши данные в порядке возрастания:

3 4 4 4 5 6 7 7 9 17.

Поскольку мы имеем четное количество значений (10), медиана является центральным значением двух точек, расположенных в середине нашей последовательности. В нашем случае это значения 5 и 6, а медианой будет значение 5,5 часов в неделю, посвященных видеоиграм. Обратите внимание на то, что мы имеем 4 значения данных (3,4,4 и 4) слева от центральных точек и 4 значения (7,7,9 и 17) справа от них.

Чтобы показать, как вычисляется медиана для нечетного количества значений данных, уберем из нашей последовательности число 17 и повторим наш анализ:

3 4 4 4 5 6 7 7 9.

Сейчас в нашем распоряжении осталась только одна центральная точка – 5. Поэтому медианой для данной последовательности будет 5 часов видеоигр в неделю. И снова мы имеем 4 значения слева и 4 значения справа от центральной точки.

4. Мода.

Теперь мы рассмотрим последнюю меру центральной тенденции – моду. Модой является наблюдение, встречающееся в наблюдении чаще всего.

Определим моду для нашего примера с видеоиграми:

3 4 4 4 5 6 7 7 9 17.

Модой является 4 часа видеоигр еженедельно – это значение встречается в нашей последовательности 3 раза. (Один набор данных может иметь более одной моды в случае, если более одного значения встречается в последовательности чаще всего).

Выводы. Если значения данных слишком велики или малы, они могут оказать весьма существенное влияние на среднее арифметическое, особенно если размер выборки невелик. Медиана не столь чувствительна к большим маленьким числам.

Возьмем набор данных, полученных в примере с видеоиграми:

3 4 4 4 5 6 7 7 9 17.

Число 17 значительно превышает все остальные значения последовательности. Среднее значение этого набора данных – 6,6, а медиана – 5,5. Если вы считает, что 17 – это нетипичный представитель полученного набора данных, то лучшим способом измерения центральной тенденции будет медиана. Мода имеет весьма ограниченное применение. Как правило, она используется для описания данных по номинальной шкале, то есть данных, сгруппированных в описательные группы, такие как пол. Если 60% наших респондентов – мужчины, тогда модой наших данных будет мужской пол.

Пример. 14000, 14700, 15300, 17100, 19300, 20800, 22400, 22900, 24000, 27500, 32400, 34800, 47200, 230000.

Среднее арифметическое = 38743 руб.

Медиана = 22650 руб.

Пример. По данным таблицы рассчитать среднюю выработку рабочего за смену.

Таблица

Ряд распределения рабочих по выработке деталей за смену

Выработка деталей за смену одним рабочим, шт	Число рабочих, человек





Всего

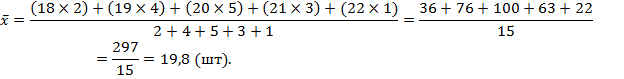
Если значения осредняемого признака заданы в виде интервалов, то при расчете средней арифметической величины в качестве значений признаков в группах принимают середины этих интервалов, в результате чего образуется дискретный ряд. При этом величины открытых интервалов условно приравниваются к интервалам, примыкающим к ним.

Пример. По данным таблицы необходимо определить среднюю заработную плату рабочих предприятия.

Таблица

Распределение рабочих предприятия по величине заработной платы

Группа рабочих по среднемесячной заработной плате, руб	Число рабочих, человек	Середина интервала, руб
До 20000
20000-30000
30000-40000
100000-300000
Итого

Средний уровень оплаты труда рабочих предприятия составляет 27720 руб.