А1. Через любые 3 точки, не лежащие на одной прямой, проходит плоскость и притом только одна.

Стр 1 из 2Следующая ⇒

Программа

год

Тема

Дата

Время

Содержание занятия

«Занимательное черчение»

2-й

«Стереометрия»

18.11.2021

30 мин теория за ПК

Изучение свойств фигур в пространстве.

1 час практика самостоятельно

аксиомы

Добрый день, ребята! Сегодня мы познакомимся с понятием стереометрии. Что такое геометрия? (Геометрия — наука о свойствах геометрических фигур. Слово «геометрия» — греческое, в переводе — «землемерие». Такое название связано с применением геометрии для измерений на местности.) Первый раздел геометрии — планиметрия.

Что такое планиметрия? (Планиметрия — раздел геометрии, в котором изучаются свойства фигур на плоскости.)

Основные понятия планиметрии (см. плакат 1) (точка, прямая: обозначение, изображение).

Н 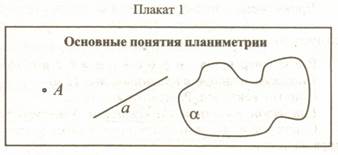еобходимо отметить, что эти понятия не определяемы, они принимаются интуитивно.

Сегодня мы приступим к изучению раздела геометрии — стереометрии.

Определение запишите в тетрадь Стереометрия — раздел геометрии, в котором изучается свойства фигур в пространстве.

Основные фигуры в пространстве: точка, прямая и плоскость.

Для обозначения точек используем прописные латинские буквы A, D, F и т. д.

Для обозначения прямых используем строчные латинские буквы f, d, h и т.д.. Или обозначаем прямую двумя прописными латинскими буквами SN.

Представление плоскости дает гладкая поверхность стены, стола.

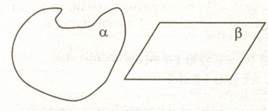Зарисуйте себе в тетрадь.

Плоскости обозначаются греческими буквами α, β, γ‚ и т.д. Плоскость как геометрическую фигуру следует представлять себе простирающейся во все стороны, не ограниченной.

Необходимо отметить, что об этих фигурах мы имеем наглядное представление, но определения этих фигур в геометрии не даются. Их свойства выражены в аксиомах. С ними мы познакомимся немного позже.

Наряду с точкой, прямой и плоскостью в стереометрии рассматривают геометрические тела, изучают их свойства, вычисляют их площади и объемы. Представление о геометрических телах дают окружающие нас предметы.

Посмотрите модели (см. плакат 2).

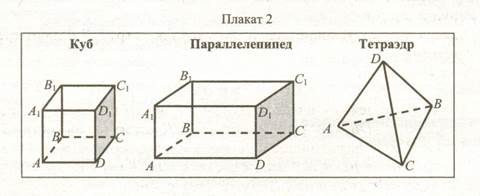
Изобразите в тетрадях куб и выделите другим цветом некоторые элементы (точки, отрезки), например: точка А, отрезок ВС.

Теперь рассмотрим аксиомы стереометрии.

· 1) Что такое аксиома? (Аксиома — это первоначальные факты геометрии, которые принимаются без доказательств и позволяют вывести из них дальнейшие факты этой науки.)

2) Какие аксиомы планиметрии вы знаете?

— через любые две точки можно провести прямую, и притом только одну.

— из трех точек прямой одна, и только одна, лежит между двумя другими.

Основные свойства точек, прямых и плоскостей, касающиеся их взаимного расположения, выражены в аксиомах:

А1. Через любые 3 точки, не лежащие на одной прямой, проходит плоскость и притом только одна.

Перепишите в тетрадь из учебника аксиому А₁. сделайте рисунок.

Важно отметить, что если взять не 3, а 4 произвольные точки, то через них может не проходить ни одна плоскость, то есть 4 точки могут не лежать в одной плоскости.

А₂. Если 2 точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

Сделайте запись и рисунки в тетрадь.

В этом случае говорят, что прямая лежит в плоскости или плоскость проходит через прямую. Из аксиомы А₂ следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются.

12 Следующая ⇒