ЗАМЕЧАНИЕ. ЗАМЕЧАНИЕ. ЗАМЕЧАНИЕ

ЗАМЕЧАНИЕ

Нулевой вектор коллинеарен любому другому вектору плоскости.

Сонаправленные и противоположно направленные векторы на плоскости

Два коллинеарных вектора и называются сонаправленными, если их направления совпадают. Сонаправленные векторы обозначаются следующим образом: . Два коллинеарные вектора и называются противоположно направленными, если их направления противоположны. Обозначение .

ЗАМЕЧАНИЕ

Считается, что нулевой вектор сонаправлен с любым другим вектором плоскости.

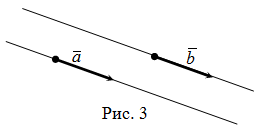
Два вектора плоскости называются равными, если они сонаправлены и их длины равны (рис. 3):

Вектор называется противоположнымк вектору , если эти векторы противоположно направлены и их длины равны.

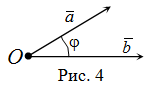
Отложим от некоторой точки на плоскости два произвольных вектора и (рис. 4). Лучи, исходящие из этой точки образуют угол , который называется углом между векторами и :

ЗАМЕЧАНИЕ

Угол между сонаправленными векторами равен (или нулю радиан), а угол между противоположно направленными векторами – (или радиан).

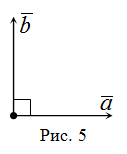
Два вектора и называются ортогональными (или перпендикулярными), если угол между ними равен ( радиан) (рис. 5).

Любой вектор на плоскости можно разложить по двум неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.

В прямоугольной системе координат для векторов выполняются следующие свойства.

1. Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.

2. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.

3. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.

Связь между координатами вектора и координатами его начала и конца.

Каждая координата вектора равна разности соответствующих координат ее конца и начала.

Каждая координата середины отрезка равна полусумме соответствующих координат его концов.

Длина вектора а с координатами х и у вычисляется по формуле:
|a ⃗| = √x² + y²

Расстояние d между точкой М₁ с координатами х₁ и у₁ и точкой М₂ с координатами х₂ и у₂ определяется по формуле:
d = √(x₂ - x₁)² +(y₂ - y₁)²

Уравнение с двумя переменными х и у называется уравнением линии L, если этому уравнению удовлетворяют координаты любой точки М, лежащей на этой линии.

В прямоугольной системе координат уравнение окружности радиуса r с центром С с координатами х₀ и у₀ имеет вид:
(x - x₁)² + (y - y₀)² = r²

Уравнение окружности радиуса r с центром в начале координат имеет вид:
x² + y² = r²

Уравнение прямой в прямоугольной системе координат является уравнением первой степени и имеет вид: ах + ву + с = 0 где а, в, с определяются по следующим формулам:

a = 2(x₁ - x₂), b = 2(y₁ - y₂), c = x₂² + y₂² - x₁² - y₁²

На все вопросы отвечу по номеру телефона.

Все ответы на задания присылать на электронный адрес:

Давыдова И.А. - alekseevna675@gmail.com

Также можно делать фото выполненных заданий и отправлять в личные сообщения в соцсети VK , WhatsApp.

Учитель	электронный адрес	Вайбер,соцсети	телефон
Давыдова И.А.	alekseevna675@gmail.com	VK https://vk.com/hell_hound666

⇐ Предыдущая 12