
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Диагностическая контрольная работа по геометрии
Диагностическая контрольная работа по геометрии
ВАРИАНТ 1
I часть (5 баллов)
При выполнении заданий 1 – 5 следует записать только ответ.
1.(1 балл) Точка А лежит вне плоскости α. Сколько можно провести через точку А прямых, параллельных плоскости α?
А) ни одной; Б) одну;
В) бесчисленное множество; Г) определить невозможно
2.(1 балл) Плоскость перпендикулярна одной из двух параллельных прямых. Как расположена вторая из этих прямых относительно данной плоскости?
А) параллельна плоскости; Б) перпендикулярна плоскости;
В) лежит в плоскости; Г) определить невозможно
3.(1 балл) Измерения прямоугольного параллелепипеда равны 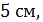
 и
и 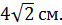 Чему равна диагональ параллелепипеда?
Чему равна диагональ параллелепипеда?
А) 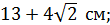 Б)
Б) 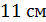 ;
;
В) 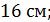 Г)
Г) 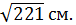
4. (1 балл) Используя изображение куба 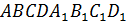 , найдите угол между прямыми
, найдите угол между прямыми 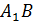 и
и 
А) 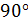 ; Б)
; Б) 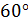 ; В)
; В) 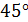 ; Г) прямые параллельны
; Г) прямые параллельны
5.  (1 балл) В пирамиде
(1 балл) В пирамиде 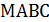 плоскости
плоскости 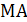 – высота. В треугольнике
– высота. В треугольнике 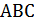
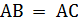 ;
; 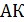 – медиана. Указать линейный угол двугранного угла при ребре ВС.
– медиана. Указать линейный угол двугранного угла при ребре ВС.
А) 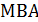 ; Б)
; Б) 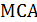 ; В)
; В) 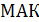 ; Г)
; Г) 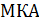
II часть (4 балла)
Решение заданий 6 – 7 должно содержать краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами.
6. (2 балла) Точка 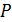 находится на расстоянии 9 см от каждой из вершин квадрата
находится на расстоянии 9 см от каждой из вершин квадрата 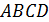 , сторона которого равна
, сторона которого равна  . Найдите расстояние от точки
. Найдите расстояние от точки 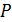 до плоскости квадрата.
до плоскости квадрата.
7. (2 балла) Даны две параллельные плоскости 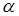 и
и 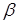 . Луч
. Луч 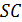 пересекает плоскость
пересекает плоскость 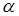 в точке
в точке 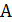 , а плоскость
, а плоскость 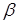 – в точке
– в точке 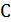 ; луч
; луч 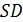 пересекает плоскость
пересекает плоскость 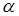 в точке
в точке  а плоскость
а плоскость 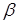 – в точке
– в точке 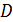 .
. 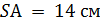 ,
,  Найдите длину отрезка АВ.
Найдите длину отрезка АВ.
III часть (3 балла)
Решение задания 8 должно содержать обоснование. В нём необходимо записать последовательные логические действия и их объяснения
8. Сторона основания правильной треугольной призмы равна 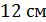 . Диагональ боковой грани образует с плоскостью основания угол
. Диагональ боковой грани образует с плоскостью основания угол 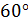 . Найдите площадь полной поверхности данной призмы.
. Найдите площадь полной поверхности данной призмы.
ВАРИАНТ 2
I часть (5 баллов)
При выполнении заданий 1 – 5 следует записать только ответ.
1.(1 балл) Даны две скрещивающиеся прямые 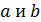 . Точки
. Точки 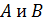 лежат на прямой
лежат на прямой 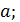 точки
точки 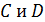 лежат на прямой
лежат на прямой 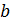 . Каково взаимное расположение прямых
. Каково взаимное расположение прямых 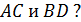
А) прямые параллельны; Б) скрещиваются;
В) пересекаются; Г) определить невозможно
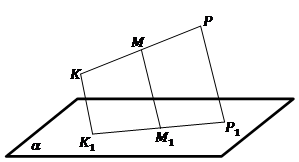 2. (1 балл) Через концы отрезка
2. (1 балл) Через концы отрезка 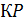 и его середину точку
и его середину точку 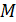 проведены параллельные прямые, пересекающие плоскость α в точках
проведены параллельные прямые, пересекающие плоскость α в точках 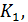
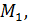
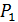 соответственно. Найти длину отрезка
соответственно. Найти длину отрезка 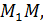 если
если 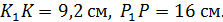
А) 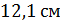 ; Б)
; Б) 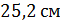 ;
;
В) 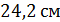 Г)
Г) 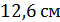
3. (1 балл) Из точки Р, удаленной от плоскости α на расстояние 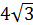 см, к этой плоскости проведена наклонная, образующая угол 60° с плоскостью α. Найти длину этой наклонной.
см, к этой плоскости проведена наклонная, образующая угол 60° с плоскостью α. Найти длину этой наклонной.
А)  ; Б)
; Б) 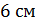 ; В)
; В) 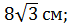 Г)
Г) 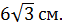
4. (1 балл) Найдите боковую поверхность прямой призмы, в основании которой лежит равнобедренный треугольник с боковой стороной 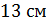 и основанием
и основанием 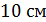 , если боковое ребро призмы равно
, если боковое ребро призмы равно 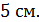
А) 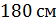 ; Б)
; Б) 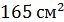 ; В)
; В) 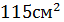 ; Г)
; Г) 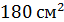
5. (1 балл) 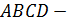 квадрат со стороной
квадрат со стороной  .
. 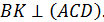 Найдите расстояние от точки
Найдите расстояние от точки 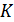 до прямой
до прямой 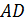 , если длина
, если длина 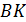 равна
равна 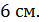
А) 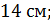 Б)
Б) 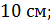 В)
В) 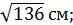 Г)
Г) 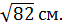
II часть (4 балла)
Решение заданий 6 – 7 должно содержать краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами.
6. (2 балла) Сторона основания правильной шестиугольной пирамиды равна 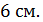 Боковые грани наклонены к основанию под углом
Боковые грани наклонены к основанию под углом 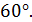 Найти площадь боковой поверхности пирамиды.
Найти площадь боковой поверхности пирамиды.
7. (2 балла) Чему равна полная поверхность прямого параллелепипеда с высотой, равной 5 см, в основании которого лежит параллелограмм со сторонами 6 см и 7 см и острым углом 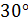 ?
?
III часть (3 балла)
Решение задания 8 должно содержать обоснование. В нём необходимо записать последовательные логические действия и их объяснения
8. Найдите высоту пирамиды 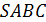 , если известно, что
, если известно, что 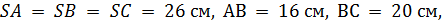
 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|