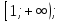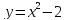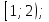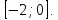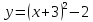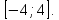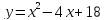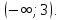- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Урок по теме: «Взаимно обратные функции. Решение задач» (Алгебра) 08.11.21.
Урок по теме: «Взаимно обратные функции. Решение задач» (Алгебра) 08.11.21.
Группа №2 МОЦИ
Пусть функция  строго монотонная (возрастающая или убывающая) и непрерывная на области определения
строго монотонная (возрастающая или убывающая) и непрерывная на области определения 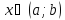 , область значений этой функции
, область значений этой функции 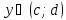 , тогда на интервале
, тогда на интервале 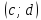 определена непрерывная строго монотонная функция
определена непрерывная строго монотонная функция  с областью значений
с областью значений 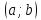 , которая является обратной для
, которая является обратной для  .
.
Другими словами, об обратной функции  для функции
для функции  на конкретном промежутке имеет смысл говорить, если на этом интервале
на конкретном промежутке имеет смысл говорить, если на этом интервале  либо возрастает, либо убывает.
либо возрастает, либо убывает.
Функции f и g называют взаимно обратными.
Зачем вообще рассматривать понятие обратных функций?
Это вызвано задачей решения уравнений  . Решения как раз и записываются через обратные функции.
. Решения как раз и записываются через обратные функции.
Рассмотрим несколько примеров нахождения обратных функций.
Начнём с линейных взаимно обратных функций.
Найти функцию, обратную для 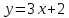 .
.
Эта функция линейная, её графиком является прямая. Значит, функция монотонна на всей области определения. Поэтому, искать обратную ей функцию будем на всей области определения.
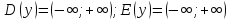 .
.
Выразим x через y (другими словами, решим уравнение 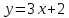 относительно x).
относительно x).
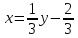 - это и есть обратная функция, правда здесь y – аргумент, а x – функция этого аргумента. Чтобы не нарушать привычки в обозначениях (это не имеет принципиального значения), переставив буквы x и y , будем писать
- это и есть обратная функция, правда здесь y – аргумент, а x – функция этого аргумента. Чтобы не нарушать привычки в обозначениях (это не имеет принципиального значения), переставив буквы x и y , будем писать 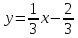 .
.
Таким образом, 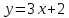 и
и 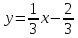 - взаимно обратные функции.
- взаимно обратные функции.
Приведём графическую иллюстрацию взаимно обратных линейных функций. 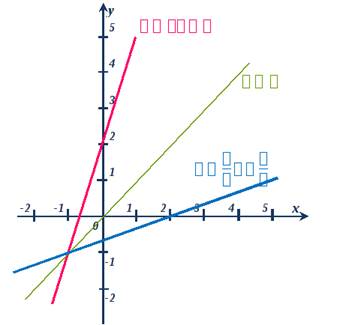
Очевидно, что графики симметричны относительно прямой  (биссектрисы первой и третьей четверти). Это одно из свойств взаимно обратных функций, о которых речь пойдёт ниже.
(биссектрисы первой и третьей четверти). Это одно из свойств взаимно обратных функций, о которых речь пойдёт ниже.
- Найти функцию, обратную
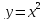 .
.
Эта функция квадратная, графиком является парабола с вершиной в точке 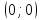 .
.
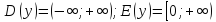 .
.
Функция возрастает при 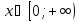 и убывает при
и убывает при 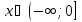 . Значит, искать обратную функцию для заданной можно на одном из двух промежутков.
. Значит, искать обратную функцию для заданной можно на одном из двух промежутков.
Пусть 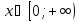 , тогда
, тогда 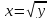 , и, меняя местами х и у, получаем обратную функцию на заданном промежутке:
, и, меняя местами х и у, получаем обратную функцию на заданном промежутке:  .
.
Найти функцию, обратную 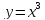 .
.
Эта функция кубическая, графиком является кубическая парабола с вершиной в точке 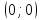 .
.
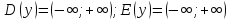 .
.
Функция возрастает при 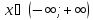 . Значит, искать обратную функцию для заданной можно на всей области определения.
. Значит, искать обратную функцию для заданной можно на всей области определения.
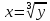 , и, меняя местами х и у, получаем обратную функцию
, и, меняя местами х и у, получаем обратную функцию 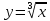 .
.
Проиллюстрируем это на графике.
Перечислим свойства взаимно обратных функций  и
и  .
.
-
 и
и  .
. - Из первого свойства видно, что область определения функции
 совпадает с областью значений функции
совпадает с областью значений функции  и наоборот.
и наоборот. - Графики взаимно обратных функций симметричны относительно прямой
 .
. - Если
 возрастает, то и
возрастает, то и  возрастает, если
возрастает, если  убывает, то и
убывает, то и  убывает.
убывает.
Для заданной функции найдите обратную функцию:
1. 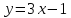
| 2. 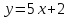
| 3. 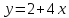
| 4. 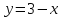
|
5. 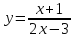
| 6. 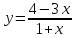
| 7. 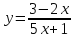
| 8. 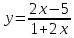
|
Для заданной функции найдите обратную и постройте графики заданной и обратной функции:
9. 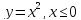
| 10. 
| 11. 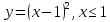
| 12. 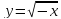
|
13. 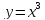
| 14. 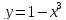
| 15. 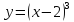
| 16. 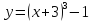
|
Выясните, существует ли обратная функция для заданной функции. Если да, то задайте обратную функцию аналитически, постройте график заданной и обратной функции:
17. 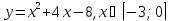
| |
19. 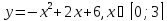
|
Найдите функцию, обратную данной. Постройте на одной системе координат графики этих взаимно обратных функций:
1. 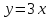
| 2. 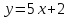
| 3. 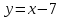
| 4. 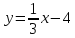
|
5. 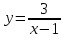
| 6. 
| 7. 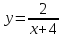
| 8. 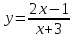
|
Является ли данная функция обратной по отношению к самой себе:
9. 
| 10. 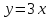
| 11. 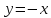
| 12. 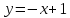
|
13. 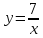
| 14. 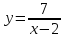
| 15. 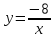
| 16. 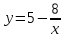
|
Задайте функцию, обратную данной и постройте её график:
1. 
| 2. 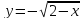
| 3. 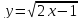
| 4. 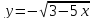
|
Рассмотрите данную функцию на каждом из указанных промежутков. Если она на этом промежутке имеет обратную функцию, то задайте её аналитически, укажите её область определения и область значений, постройте её график.
|
|
|
|
На каждом из указанных промежутков найдите, если это возможно, функцию, обратную данной:
- на
 ; на
; на 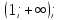 на
на 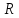 ;
; - на
 ; на
; на 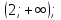 на
на 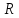 ;
; - на
 ; на
; на  на
на 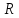 ;
; - на
 ; на
; на  на
на 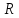 ;
;
Даны взаимно обратные функции  и
и 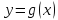 .
.
-
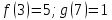 . Решите уравнения:
. Решите уравнения: 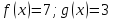
-
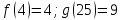 . Решите уравнения:
. Решите уравнения: 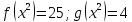
-
 . Решите уравнения:
. Решите уравнения: 
-
 . Решите уравнения:
. Решите уравнения:
Постройте график функции и определите, существует ли для неё обратная функция. Если да, то на том же чертеже постройте график обратной функции и задайте её аналитически.
1. 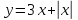
| 2. 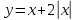
| 3. 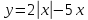
| 4. 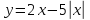
|
5. 
| 6. 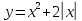
| 7. 
| 8. 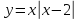
|
Дана функция  , график которой изображён на рисунке. Постройте график обратной функции и найдите области определения и области значений обоих функций.
, график которой изображён на рисунке. Постройте график обратной функции и найдите области определения и области значений обоих функций.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|