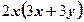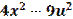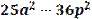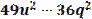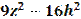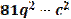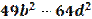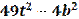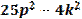- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Разложение многочлена на множители
Сокращение рациональных дробей
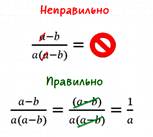 Для этого повторяем следующую тему:
Для этого повторяем следующую тему:
Разложение многочлена на множители
ЧИТАЕМ ТЕОРИЮ.
Выполняем упражнения
(из 20 заданий можно сделать 10 заданий)
вынесение общего множителя за скобки
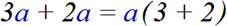
−2a − 4b − 6c = −2(a + 2b + 3c)
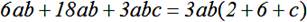
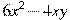 вынесли за скобки множитель
вынесли за скобки множитель 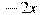 . В каком случае преобразование выполнено верно?
. В каком случае преобразование выполнено верно?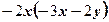 2)
2) 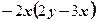
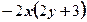 4)
4) 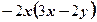
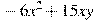 вынесли за скобки множитель
вынесли за скобки множитель 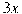 . В каком случае преобразование выполнено верно?
. В каком случае преобразование выполнено верно?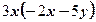 2)
2) 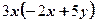
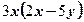 4)
4) 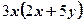
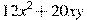 вынесли за скобки множитель
вынесли за скобки множитель 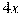 . В каком случае преобразование выполнено верно?
. В каком случае преобразование выполнено верно?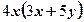 2)
2) 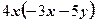
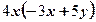 4)
4) 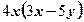
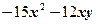 вынесли за скобки множитель
вынесли за скобки множитель 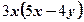 2)
2) 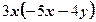
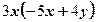 4)
4) 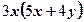
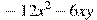 вынесли за скобки множитель
вынесли за скобки множитель 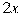 . В каком случае преобразование выполнено верно?
. В каком случае преобразование выполнено верно?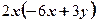 2)
2) 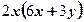
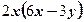 4)
4) 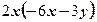
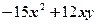 вынесли за скобки множитель
вынесли за скобки множитель 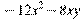 вынесли за скобки множитель
вынесли за скобки множитель 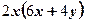 2)
2) 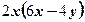
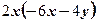 4)
4) 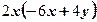
 вынесли за скобки множитель
вынесли за скобки множитель 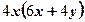 2)
2) 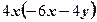
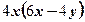 4)
4) 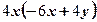
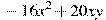 вынесли за скобки множитель
вынесли за скобки множитель 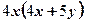 2)
2) 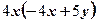
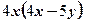 4)
4) 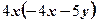
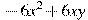 вынесли за скобки множитель
вынесли за скобки множитель 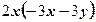 2)
2) 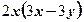
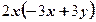 4)
4)