Примеры решения задач на законы сохранения

8 Примеры решения задач на законы сохранения

При дистанционном обучении на первое место по значимости выходит ваша самостоятельная работа по проработке готовых решений.

При изучении готовых решений происходит освоение и запоминание метода (алгоритма) решений. Это позволяет вам потом самостоятельно решать задачи.

17. Два шара с массами m₁ = 0,2 кг и m₂ = 0,1 кг подвешены на параллельных нитях одинаковой длины так, что они соприкасаются. Первый шар отклоняют на высоту h₀ = 4,5 см и отпускают. На какую высоту h поднимутся шары после удара, если удар: а) упругий; б) неупругий?

Решение. Для решения задачи воспользуемся законами сохранения импульса и механической энергии. Система шаров не является замкнутой, т.к. на шары действуют силы тяжести и натяжения нитей. Но во время удара эти силы направлены вертикально и скомпенсированы. Поэтому проекция импульса на горизонтальное направление сохраняется. Рассмотрим виды удара по очереди.

а) Упругий удар. При таком ударе выполняются законы сохранения импульса и энергии. Пусть v₁ – скорость первого шара в момент удара, и 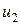– скорости первого и второго шаров непосредственно после удара. Согласно законам сохранения импульса и энергии имеем

, . (1)

Решая эту систему уравнений, находим скорости шаров после удара

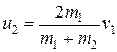, . (2)

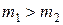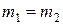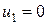Т.к. , то, как видно из (2) оба шара после удара будут двигаться в одном направлении. Если , то , а .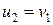

Скорость первого шара до удара найдем из закона сохранения энергии, приравняв потенциальную энергию поднятого шара, кинетической энергии в момент удара

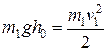Отсюда получим

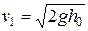= 9,4 м/с, = 3,13 м/с, 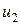= 12,5 м/с. (3)

Высоту, на которую поднимутся шары после удара, найдем из того же закона сохранения энергии

= 1,5 см, = 6 см.

б) Неупругийудар. При таком ударе шары соединяются вместе, а при ударе выполняется только закон сохранения импульса

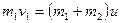, (4)

где u – скорость шаров после удара. Отсюда скорость шаров после удара

. (5)

Скорость первого шара до удара найдем по формуле (3) и, подставив в (5) определим скорость шаров после удара

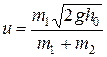= 0,63 м/с.

Высоту подъема шаров найдем из закона сохранения энергии по формуле

= 2 см.