
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Примеры решения задач на работу, мощность и энергию
7 Примеры решения задач на работу, мощность и энергию
При дистанционном обучении на первое место по значимости выходит ваша самостоятельная работа по проработке готовых решений.
При изучении готовых решений происходит освоение и запоминание метода (алгоритма) решений. Это позволяет вам потом по примерам самостоятельно решать задачи.
20.Насос должен перекачать воду из одного резервуара в другой. Первый резервуар до краев наполнен водой и имеет такие размеры: площадь дна 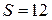 м2, высота
м2, высота 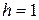 м. Верхние границы резервуаров находятся на разных уровнях так, что расстояние от верха полного до верха пустого составляет
м. Верхние границы резервуаров находятся на разных уровнях так, что расстояние от верха полного до верха пустого составляет 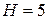 м. Определить: сколько времени необходимо насосу, если его мощность
м. Определить: сколько времени необходимо насосу, если его мощность 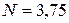 кВт и коэффициент полезного действия
кВт и коэффициент полезного действия 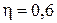 .
.
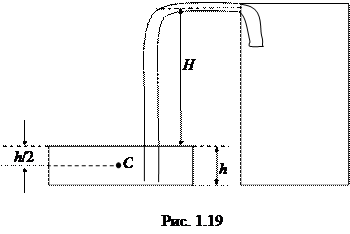 |
Решение. Работа, которую нужно совершить для того, чтобы перекачать воду из первого резервуара во второй, равна изменению ее потенциальной энергии. В этом случае центр масс воды С массы
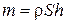 нужно поднять на высоту
нужно поднять на высоту 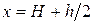 (см. рис. 1.19), т.е. работа
(см. рис. 1.19), т.е. работа
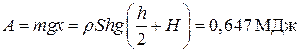 .
.
Время, необходимое для этого,
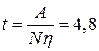 мин.
мин.
19. Какую мощность P развивает двигатель автомобиля массой m = 1 т, если известно, что автомобиль едет с постоянной скоростью v = 36 км/ч: а) по горизонтальной дороге; б) в гору с уклоном 5 м на каждые 100 м пути; в) под гору с тем же уклоном? Коэффициент трения m = 0,07.
Решение. Как известно, мощность равна отношению работы 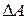 ко времени
ко времени 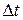 , за которое совершена работа, и ее можно определить по формуле
, за которое совершена работа, и ее можно определить по формуле
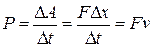 ,
,
где F – действующая на тело сила, 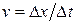 – скорость тела.
– скорость тела.
Выразим силу F для всех случаев из второго закона Ньютона.
а) Так как v = const, то сила тяги автомобиля F скомпенсирована силой трения 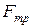 , которая по закону трения
, которая по закону трения 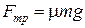 , т.е.
, т.е. 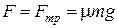 . Следовательно, при движении автомобиля по горизонтальной дороге мощность равна
. Следовательно, при движении автомобиля по горизонтальной дороге мощность равна
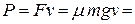 6,9 кВт.
6,9 кВт.
б) При движении в гору сила тяги двигателя противодействует скатывающей силе 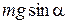 и силе трения
и силе трения 
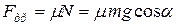 , где a – угол наклона горы к горизонту, который найдем по формуле
, где a – угол наклона горы к горизонту, который найдем по формуле 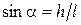 =0,05 Следовательно,
=0,05 Следовательно, 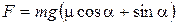 . Тогда для мощности получим
. Тогда для мощности получим
 = 11,8 кВт.
= 11,8 кВт.
в) При движении под гору скатывающая сила будет направлена по направлению силы тяги, а сила трения против движения. Поэтому сила тяги будет равна 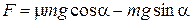 . Мощность найдем по формуле
. Мощность найдем по формуле

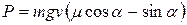 = 2 кВт.
= 2 кВт.
16. Камень массой m = 0,2 кг бросили под углом α = 60˚ к горизонту со скоростью v0 = 15 м/с. Найти кинетическую 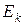 , потенциальную
, потенциальную 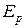 и полную энергию
и полную энергию 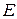 камня спустя время t = 1 с после начала движения и в высшей точке траектории. Сопротивлением воздуха пренебречь.
камня спустя время t = 1 с после начала движения и в высшей точке траектории. Сопротивлением воздуха пренебречь.
Решение. При движении камня без сопротивления воздуха полная механическая энергия сохраняется, а его траектория будет параболой (рис. 1.17). Проекции скорости на горизонтальную и вертикальную оси х и у координат и координаты камня при таком движении изменяются по закону
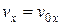 ,
, 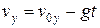 ,
, 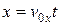 ,
, 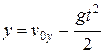 , (1)
, (1)
где 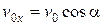 и
и 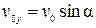 – начальные значения скорости.
– начальные значения скорости.
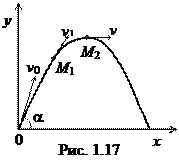 Кинетическую, потенциальную и полную энергию камня можно рассчитать по формулам
Кинетическую, потенциальную и полную энергию камня можно рассчитать по формулам
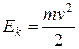 ,
, 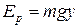 ,
, 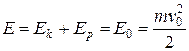 ,
,
где 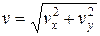 – текущая скорость камня.
– текущая скорость камня.
Для момента времени 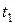 = 1 с в точке М1 имеем:
= 1 с в точке М1 имеем:
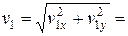 8,15 м/с,
8,15 м/с, 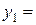 8,1 м,
8,1 м,
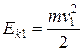 = 6,5 Дж,
= 6,5 Дж, 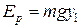 = 16 Дж,
= 16 Дж, 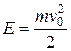 = 22,5 Дж.
= 22,5 Дж.
В верхней точке М2 траектории 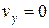 и из второго уравнения (1) найдем время
и из второго уравнения (1) найдем время 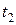 подъема камня
подъема камня
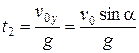 = 1,3 с.
= 1,3 с.
Высоту подъема h камня определим по формуле
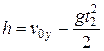 = 8,4 м.
= 8,4 м.
Кинетическую и потенциальную энергию в точке М2 рассчитаем по формулам
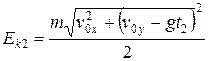 = 5,6 Дж,
= 5,6 Дж, 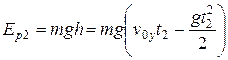 = 16,9 Дж.
= 16,9 Дж.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|