
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Лекция 7. Критерий Рауса
Лекция 7
Устойчивость линейных САР
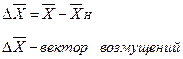
Для устойчивого состояния (математического) 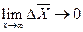
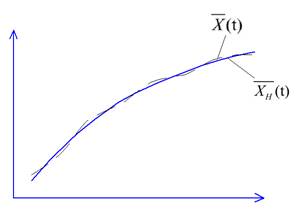
Движение называется устойчивым по Ляпунову, если при небольших изменениях начальных значений 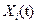
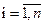 возмущенное движение
возмущенное движение 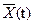 при
при 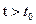 как угодно мало отличается от невозмущенного движения
как угодно мало отличается от невозмущенного движения 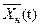
Асимптотическая устойчивость
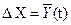
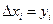
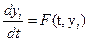 ,
, 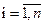 (*)
(*)

Линеаризуем (*) в районе номинального значения
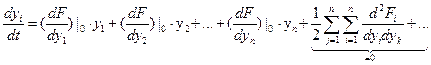
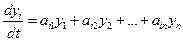 (2*)
(2*)
Коэффициенты зависят от параметров системы
1) Самый простой случай 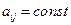 (можно аналитически)
(можно аналитически)
2) 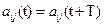
3) 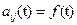 (только численное решение)
(только численное решение)
Условия, при которых можно использовать решение линеаризующих уравнений (*) при исследовании устойчивости движения без опаски ошибиться сформулированы Ляпуновым в следующих теоремах.
Теорема 1
Если все корни характеристического уравнения1-го приближения имеют вещественные части отрицательные, то невозмущенное движение асимптотически устойчиво (при малых отклонениях), независимо от отброшенных частей.
Теорема 2
Если среди корней 1-го приближения есть хотя бы один с положительной вещественной частью, то движение неустойчиво. Не зависит от отброшенной части.
Теорема 3
Если вещественные части равны 0, то нельзя однозначно сказать об устойчивости, пограничный случай.
Важно научиться судить об устойчивости без непосредственного решения ДУ. В дальнейшем исследуем именно однородную систему:
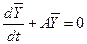
Другая форма записи:
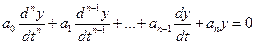 (3*)
(3*)
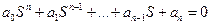 (4*)
(4*)
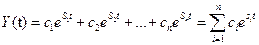
Предположим: k-число действительных корней
(n-k) – комплексных
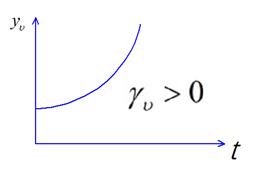
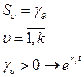
Неустойчивое положение
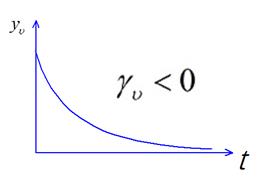
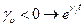
Устойчивое положение
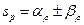
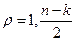
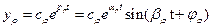
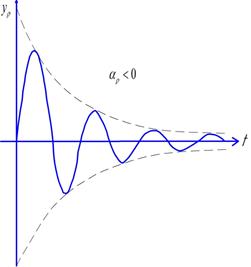
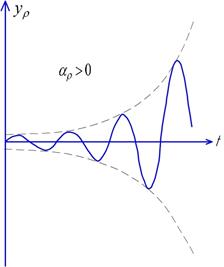
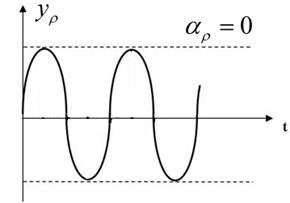
- устойчивый колебательный процесс
Все пограничные состояния системы будем относить к неустойчивому движению.
Часто удобно представить характерное уравнение в следующем виде:
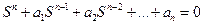
Если все корни найдены:
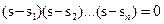
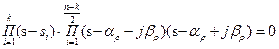
Важное значение приобретают правила, позволяющие определять устойчивость системы, минуя вычисление корней. Это правило называется критериями устойчивости.
Критерии устойчивости подразделяются на алгебраические и частотные.
Критерий Вышнеградского для системы 3-го порядка
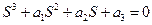
1) 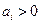
Он делал следующие замены:
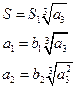
Отсюда, 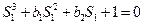
Рассмотрим предельные случай, когда уравнение имеет:
1-ый корень: 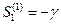
2-ой 3-ий корень: 
Тогда:
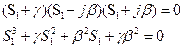
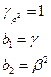
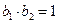
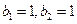
В итоге, получим гиперболу
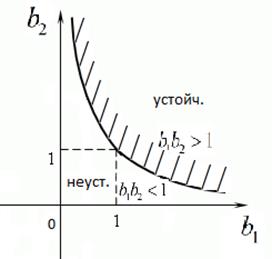
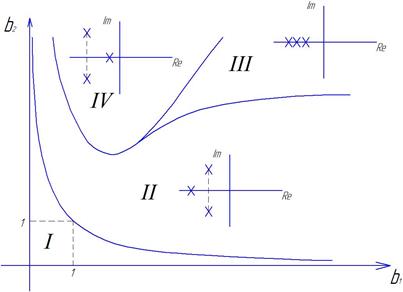
Критерий Рауса
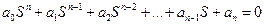

где 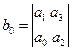
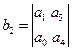
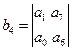
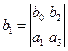
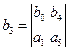
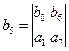
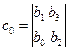
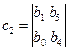
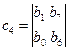
Условие устойчивости является положительность 1-ого столбца таблицы Рауса
Все коэффициенты, которые не вычисляются равны 0.
Пример: 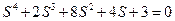
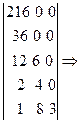 1-ый столбец положителен, поэтому система устойчива
1-ый столбец положителен, поэтому система устойчива
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|