Теоретический материал для самостоятельного изучения

08.11.2021
Тема: Прямая и обратная пропорциональность. Решение задач.
Цель: продолжить изучать прямую и обратную пропорциональность;
рассмотреть практическое применение прямой и обратной пропорциональности.
Задачи: научиться применять полученные теоретические знания при решении различного типа математических задач.

Теоретический материал для самостоятельного изучения

Прямая пропорциональность.

Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.

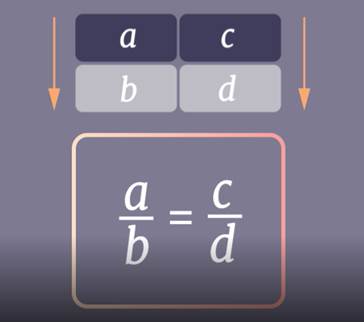
Обратная пропорциональность.

Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.

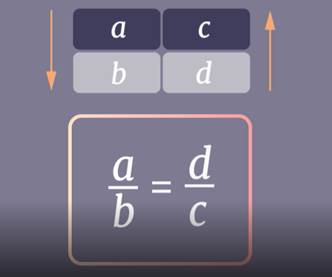
Для решения задач на пропорциональную зависимость, удобно составить таблицу или сделать краткую запись условия.

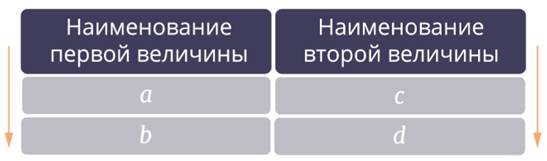
Столбцы таблицы соответствуют наименованиям зависимых величин.

Строки таблицы соответствуют значениям величин при первом и втором измерении.

Одинаково направленные стрелки показывают прямо пропорциональную зависимость, противоположно направленные – обратно пропорциональную.

Задача.

Поезд, скорость которого 55 км/ч, был в пути 5 часов. За сколько часов пройдёт этот же участок пути товарный поезд, скорость которого 45 км/ч?

Решение.

При постоянном пути скорость и время движения обратно пропорциональны.

Допустим, товарный поезд пройдёт этот же путь со скоростью 45 км/ч за x ч.

Сделаем краткую запись условия.

Задача.

Двигаясь с постоянной скоростью, велогонщик проезжает 40 метров за 3 с. Какой путь проедет велогонщик за 45 с?

Решение.

При постоянной скорости путь прямо пропорционален времени движения.

Пусть х м проедет велогонщик за 45 с.

Сделаем краткую запись условия.

Задача.

Усилие при восхождении на высоту 600 м равно усилию, требуемому для перехода 25 км по равнине. Турист поднялся в горы на 792 м. Какому расстоянию на равнине соответствует этот подъём?

Решение:

Решение.

Задача.

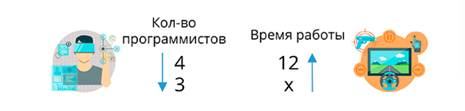
Четыре программиста могут написать игру за 12 месяцев. За сколько месяцев эту работу могут выполнить три программиста?

Решение.

Количество программистов и скорость написания игры – это обратно пропорциональная зависимость.

Разбор заданий тренировочного модуля

№ 1. Подстановка элементов в пропуски в тексте.

Подставьте нужные элементы в пропуски.

Пешеход шёл 3 часа со скоростью 8 км/ч. За сколько часов он пройдёт то же расстояние со скоростью 6 км/ч?

№ 2. Подстановка элементов в пропуски в таблице.

Заполните таблицу.

Поезд движется со скоростью 45 км/ч. Какое расстояние он пройдёт, если будет в пути 3 ч; 4 ч; 5 ч; 6 ч.