
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Алгоритмы решения задач Импульс.
6 Алгоритмы решения задач Импульс.
Законы сохранения энергии и импульса являются фундаментальными законами природы. Особое значение этих законов для решения задач и в исследованиях связано с такими факторами:
Законы сохранения разрешают получить ряд общих выводов о разных свойствах механических процессов без детального их рассмотрения с использованием уравнений движения.
Законы сохранения, в некоторых случаях, можно использовать даже тогда, когда силы, действующие внутри системы, вообще неизвестны. В этом случае законы сохранения являются единственным инструментом исследования.
Даже в тех случаях, когда силы известны, законы сохранения могут существенно помочь при решении многих задач о движении частиц. Эти задачи могут быть решены с помощью уравнений движения, но использование законов сохранения позволяет получить решение наиболее простым путем. Поэтому при решении задач целесообразно придерживаться такого алгоритма: прежде всего применяют законы сохранения, и лишь убедившись, что их недостаточно, переходят к решению с помощью уравнений движения.
Импульс, как и кинетическая энергия тела, зависит от выбора системы отсчета и изменяется при переходе от одной системы отсчета к другой. Поэтому при записи уравнений, которые выражают законы сохранения импульса и энергии, надо рассматривать движение всех тел в одной и той же инерциальной системе отсчета.
Закон сохранения импульса связывает начальное и конечное значения импульса замкнутой системы. Это позволяет исключить из рассмотрения внутренние силы (силы взаимодействия частей системы) и применить закон в тех задачах, в которых силы взаимодействия между отдельными телами системы являются величинами переменными, причем характер их изменения во времени – сложный или даже неизвестный (например, силы, которые возникают при столкновении).
Надо помнить, что уравнение (4.5), которое выражает закон сохранения импульса, является векторным. Поэтому при нахождении вектора 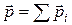 надо использовать правило сложения векторов или выбрать оси и записать закон сохранения импульса в проекциях на эти оси:
надо использовать правило сложения векторов или выбрать оси и записать закон сохранения импульса в проекциях на эти оси:
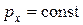 ,
, 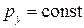 , ...
, ...
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|