Хелпикс

Главная

Контакты

Случайная статья



Решение тригонометрических неравенств, сводящихся  к простейшим.

Стр 1 из 2Следующая ⇒


 

Группа 2Б   Дата 08.11.21г.

Тема: Простейшие тригонометрические неравенства.

План

1. Простейшие тригонометрические неравенства.

 

Определение. Неравенство, в котором неизвестная переменная находится под знаком тригонометрической функции, называется тригонометрическим неравенством.

Определение. Кпростейшим тригонометрически неравенствамотносятся следующие 16 неравенств:

 

sinx>a, sinx≥a, sinx<a, sinx≤a,
cosx>a, cosx≥a, cosx<a, cosx≤a,
tgx>a, tgx≥a, tgx<a, tgx≤a,
ctgx>a, ctgx≥a, ctgx<a, ctgx≤a.

 

Здесь x - является неизвестной переменной,

a - может быть любым действительным числом.

 

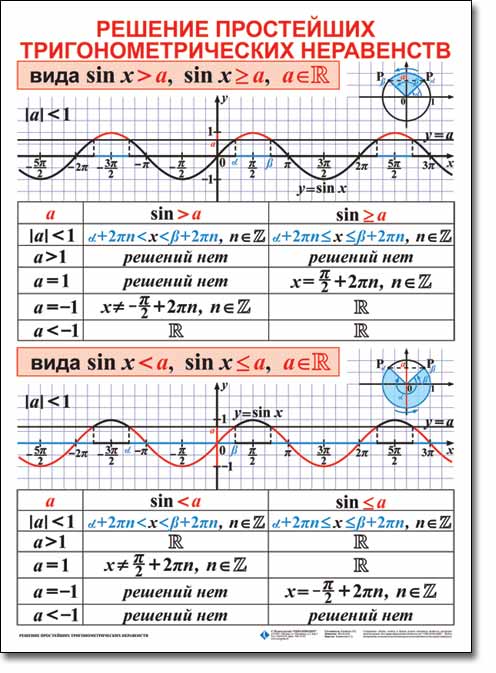
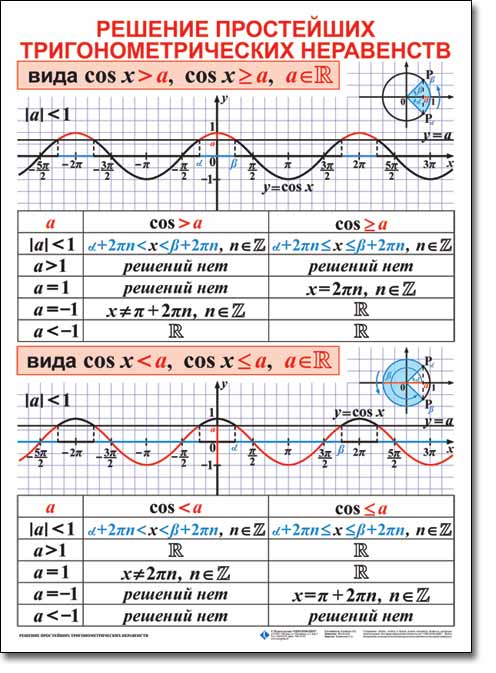
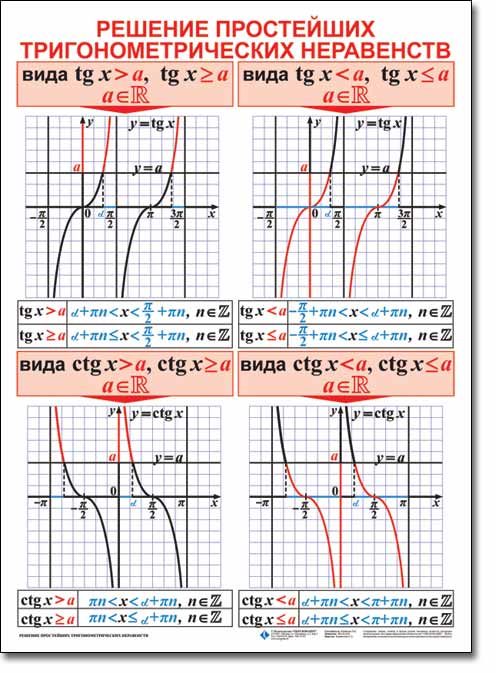
Рассмотрим примеры решения простейших неравенств

                                               

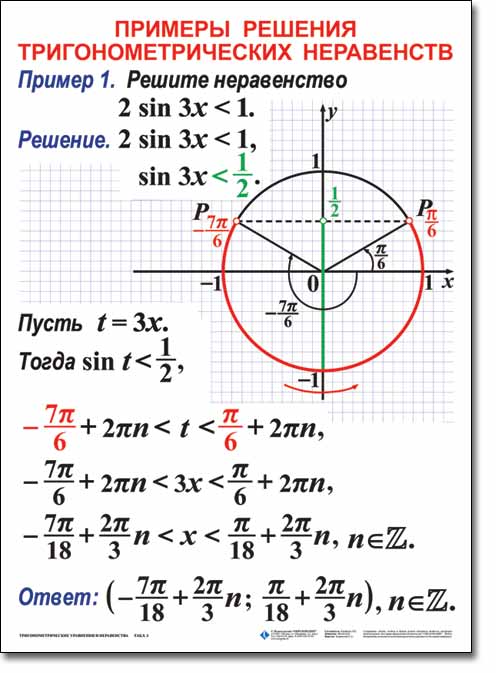
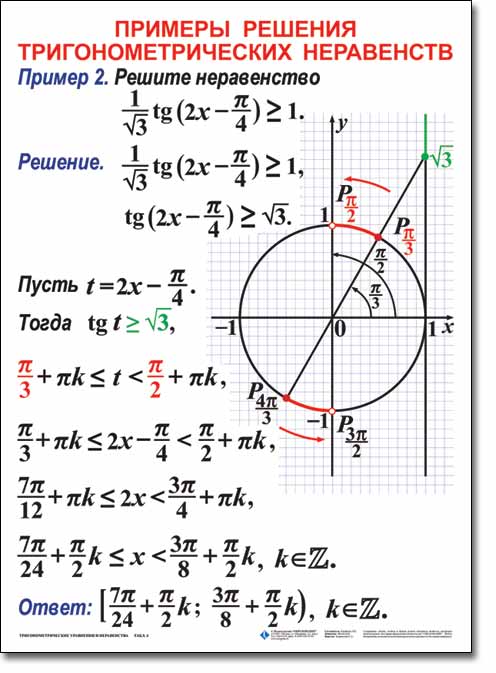
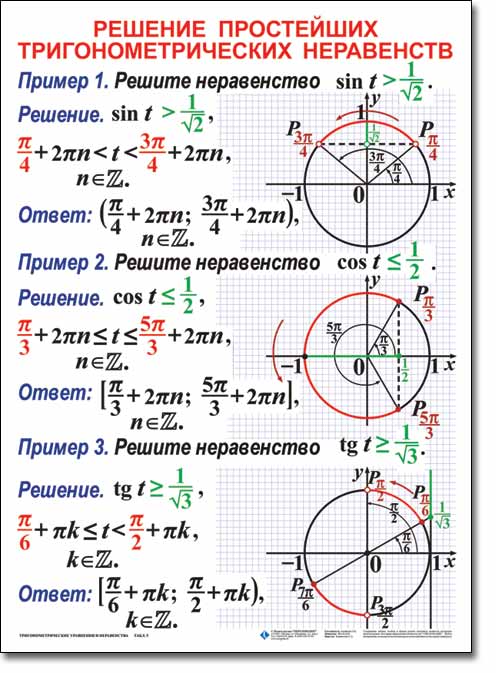
Решение тригонометрических неравенств, сводящихся  к простейшим.

Если аргумент функции неравенства представлен не просто переменной, а целым выражением содержащим неизвестную, то речь уже идет о сложном неравенстве.

Ход и порядок его решения несколько отличаются от способов описанных выше. Допустим необходимо найти решение следующего неравенства:

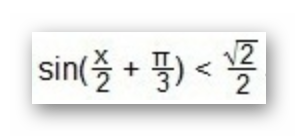
Графическое решение предусматривает построение обычной синусоиды y = sin x по произвольно выбранным значениям x. Рассчитаем таблицу с координатами для опорных точек графика:

.

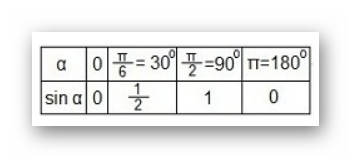
Для простоты поиска решения заменим сложный аргумент функции

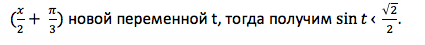
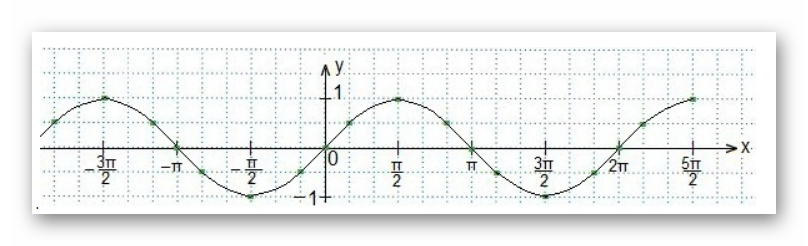
Пересечение двух графиков позволяет определить область искомых значений, при которых выполняется условие неравенства.

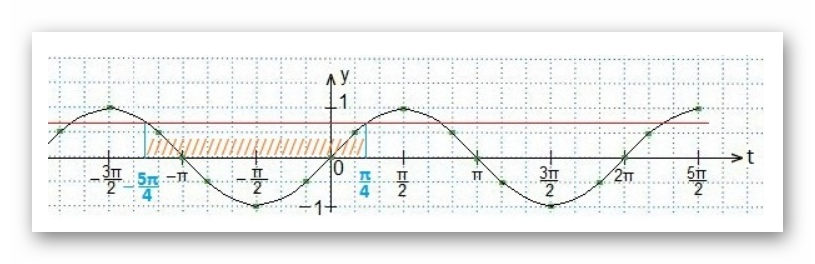
Найденный отрезок является решением для переменной t:

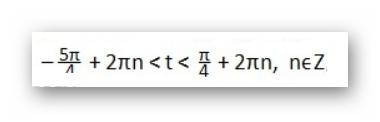
Подставляем вместо t значение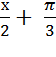

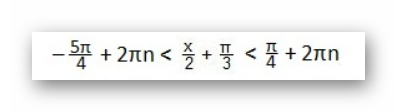
Решить двойное неравенство достаточно просто, нужно перенести π/3 в крайние части уравнения и произвести требуемые вычисления:

Ответ на задание будет выглядеть как интервал для строгого неравенства:


12Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.