Примеры и разборы решения заданий тренировочного модуля

Примеры и разборы решения заданий тренировочного модуля

Пример 1. Выясним, является ли функция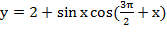

чётной или нечётной?

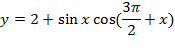
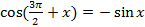
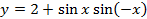
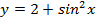
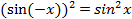
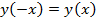
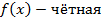
Пример 2.Доказать, что число 2π является наименьшим положительным периодом функции y=cos x

Пусть Т>0 – период косинуса, т.е. для любого х выполняется равенство cos (x+T)= cos x. Положив х=0, получим cos T=1. Отсюда Т=2πk, x∈R. Так как Т>0, то может принимать значения 2π, 4π, 6π,…, и поэтому период не может быть меньше 2π

⇐ Предыдущая 12