Для студентов 296 группы. Формула полной вероятности.. Р (А)=Р (А/Н1) · Р (Н1) + Р (А/Н2) · Р (Н2) + . + Р (А/Нn) · Р (Нn). Вероятность события А равна сумме произведений условной вероятности события А по каждой из гипотез на вероятность самих гипотез

Для студентов 296 группы

6.Формула полной вероятности.

Предположим, что событие А может наступить только с одним из группы несовместных событий Н₁, Н_2, ... Н_n . Эти события называют гипотезами. Тогда справедлива формула полной вероятности.

Р (А)=Р (А/Н1) · Р (Н1) + Р (А/Н2) · Р (Н2) + ... + Р (А/Нn) · Р (Нn)

Вероятность события А равна сумме произведений условной вероятности события А по каждой из гипотез на вероятность самих гипотез.

Задача.

Имеется три урны. Первая содержит 2 черных и 3 белых шара, вторая – 2 черных и 1 белый шар, третья урны содержит 4 черных шара. Сначала произвольно выбирают урну, а затем из нее наугад извлекают один шар. Какова вероятность того, что будет выбран белый шар.

Решение.

Пусть событие А состоит в том, что белый шар будет извлечен из произвольной урны, а Н₁, Н_2,Н₃ – гипотезы, что он принадлежит соответственно первой, второй и третьей урне. Тогда по формуле полной вероятности найдем вероятность события А.

Р(А) = Р(А/Н₁)Р(Н₁)+ Р(А/Н₂)Р(Н₂) + Р(А/Н₃)Р(Н₃)

Вероятность того, что выбрана 1 урна Р(Н₁) = 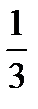. Вероятность того, что выбрана 2 урна Р(Н₂) = 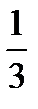. Вероятность того, что выбрана 3 урна Р(Н₃) = 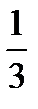. Вероятность того, что белый шар принадлежит первой урне Р(А/Н₁) = , вероятность того, что белый шар принадлежит второй урне Р(А/Н₂) = 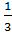, а вероятность того, что белый шар принадлежит третьей урне Р(А/Н₃) = 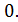По формуле полной вероятности найдем вероятность взятия белого шара. Р(А) = 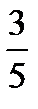∙ 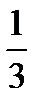+ 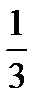∙ 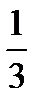=0,3

Ответ. Р(А) = 0,3