Тема: «Параллелепипед. Куб»

11.11.2021

Задание высылать в личном сообщении в вк или на почту SHPAK.IRINA.S@yandex.ru

Перед каждым заданием в тетради пишем ФИО, дата, тема урока.

Написать краткий конспект и задачи (не забываем и про чертежи).

Тема: «Параллелепипед. Куб»

Теоретическая часть:

Параллелепипед – это поверхность, составленная из двух равных параллелограммов ABCDи A₁B₁C₁D₁и четырех параллелограммов; обозначается: ABCDA₁B₁C₁D₁

Грани параллелепипеда – это параллелограммы, из которых составлен параллелепипед.

Вершины параллелепипеда – вершины параллелограммов.

Параллелепипед имеет 6 граней, 12 ребер и 8 вершин.

Две грани параллелепипеда, имеющие общее ребро, называются смежными, а не имеющие общих ребер – противоположными.

Диагональ параллелепипеда – это отрезок, соединяющий противоположные вершины.

Часто выделяют какие-нибудь две противоположные грани и называют их основаниями, а остальные грани – боковыми гранями параллелепипеда.

Боковые ребра – ребра параллелепипеда, не принадлежащие основаниям.

Свойство 1. Противоположные грани параллелепипеда параллельны (лежат в параллельных плоскостях) и равны.

Свойство 2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

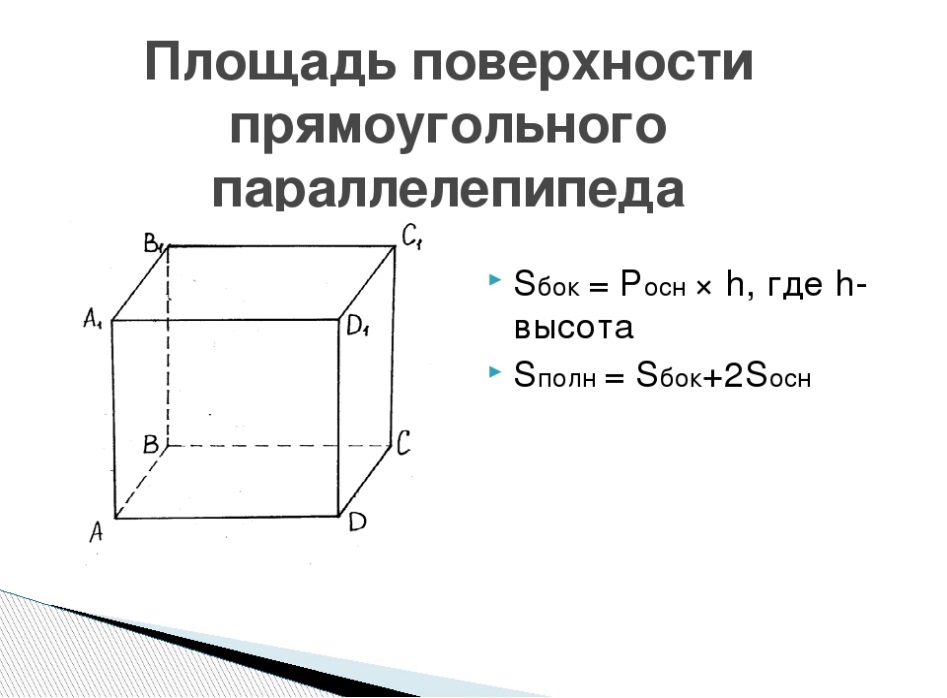
Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.

Свойство 3. В прямоугольном параллелепипеде все шесть граней – прямоугольники.

Свойство 4. Все двугранные углы прямоугольного параллелепипеда – прямые.

Измерения прямоугольного параллелепипеда – длины трех ребер, имеющих общую вершину. В обыденной практике это «длина», «ширина» и «высота».

Теорема: квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

Следствие: диагонали прямоугольного параллелепипеда равны.

Куб – это прямоугольный параллелепипед, у которого все три измерения равны.

Все грани куба – равные друг другу квадраты.

Практическая часть:

Задача 1

Измерения прямоугольного параллелепипеда равны 4 см, 8 см и 6 см. Вычислить площадь поверхности и найти длину ребер.

Решение

1) S_пов=2(ab+ac+bc);

S_пов= 2(4·8+4·6+8·6) = 2(32+24+48)=2·104=208 (см²)

2) L=4(a+b+c);

L=4(4+8+6)=4·18=72 (см)

Ответ:208 см²; 72 см

Задача 2

Решение

Пусть AB=5, AD= , AA₁=7.

1) НайдемB₁D

B₁D²=AB²+AD²+AA₁²;

B₁D²=5²+( )²+7²=25+47+49=121;

B₁D=11

2) Найдем sinα

B₁B=A₁A=7;

Ответ: 11;