Контакты

Случайная статья

Тема. Метод введения параметра. Решения уравнения относительно параметра как новой переменной.

18.11.21

Тема. Метод введения параметра. Решения уравнения относительно параметра как новой переменной.

https://yandex.fr/video/preview/7435172259639603660

Метод введения параметра

Метод введения параметра позволяет нестандартное уравнение привести к уравнению привычного вида (например, к квадратному уравнению).

Рассмотрим конкретные примеры уравнений, которые можно решить методом введения параметра.

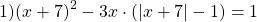
ОДЗ: x∈R.

Так как

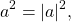
перепишем уравнение в виде

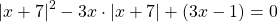
Введём параметр. Пусть

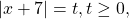
тогда

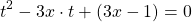
Получили квадратное уравнение относительно переменной t. Здесь

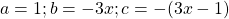
Находим дискриминант

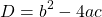
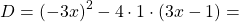
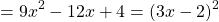
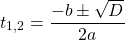
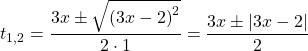
В данном случае раскрытие модуля с любым знаком приводит к одним и тем же корням

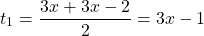
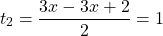
Обратная замена

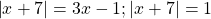
При x< -7

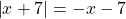
и

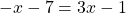
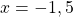
-1,5∉(-∞; -7).

2) При x≥ -7

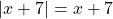
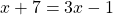
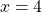
4∈[-7; ∞).

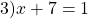
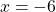
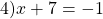
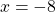
Ответ: -8; -6; 4.

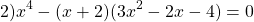
ОДЗ: x∈R.

Если раскрыть скобки и привести подобные слагаемые, придём к уравнению 4-й степени.

Рассмотрим другой подход.

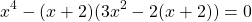
Пусть x+2=t, тогда

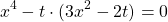
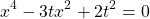
Это уравнение можно решать и как квадратное уравнение относительно переменной t, и как биквадратноеотносительно переменной x — результат получим один и тот же.

Решим его как квадратное относительно t (чтобы не вводить ещё одну переменную).

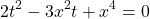
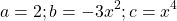
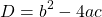
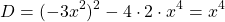
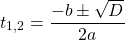
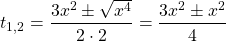
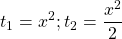
Обратная замена

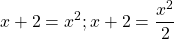
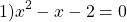
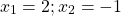
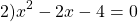
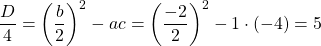
Ответ:

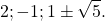
Метод введения параметра используют в самых разных разделах алгебры. В частности, введением параметра могут быть решены некоторые тригонометрические, иррациональные, логарифмические и показательные уравнения.(это будем решать дальше)

Рассмотрите внимательно решения уравнения , способом введения новой переменной.

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.