Конспект урока Умножение дробей. Возведение дроби в степень

15.11.2021 Алгебра 8 класс

Тема: Умножение дробей. Возведение дроби в степень.

Ход урока

Организационный момент Мы сегодня начинаем изучать тему «Произведение и частное дробей». На её изучение у нас 5 часов. 22.11 контрольная работа по этой теме.

Подготовка у уроку. Открыли тетрадь, записали число, Дистанционное обучение, тема урока.

Работа по теме урока: Формулы и примеры записываем в рабочую тетрадь.

Конспект урока "Умножение дробей. Возведение дроби в степень"

Для начала давайте вспомним правило умножения обыкновенных дробей.

Для того чтобы умножить дробь на дробь, надо числитель умножить на числитель, а знаменатель на знаменатель и первое произведение записать в числителе новой дроби, второе – в знаменателе.

Например

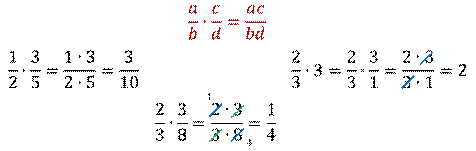
Аналогичным образом происходит умножение рациональных дробей. Давайте докажем, что это правило на самом деле действует при умножении рациональныхдробей.

Иначе говоря, докажем, что произведение двух рациональных дробейтождественно равно дроби, у которой числитель равен произведению числителей, а знаменатель – произведению знаменателей перемножаемых дробей при любых допустимых значениях переменных, кроме b равное нулю и d равное нулю.

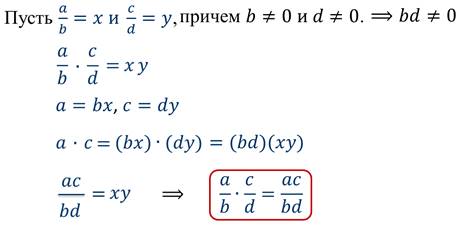
Получили, что равенство верно при любых допустимых значениях переменных, т.е. является тождеством.

Правило умножения рациональных дробей:

Чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе – знаменателем дроби.

В буквенном виде это правило записывают так:

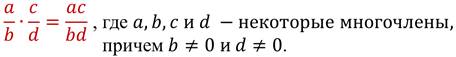
Это правило выполняется и когда произведение трёх и более рациональных дробей.

Прежде чем выполнять умножение рациональных дробей, полезно их числители и знаменатели разложить на множители. Это облегчит сокращение той рациональной дроби, которая получится в результате умножения.

Пример 1: умножить дроби.

Решение:

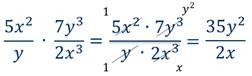
Пример 2: умножить дроби.

Решение:

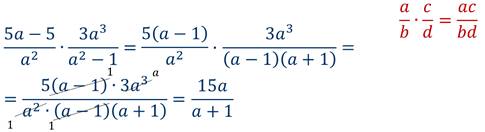
Пример 3: Представить произведение дробей в виде рациональной дроби.

Решение:

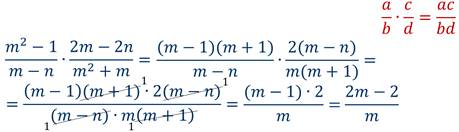
Пример 4: выполнить умножение.

Решение:

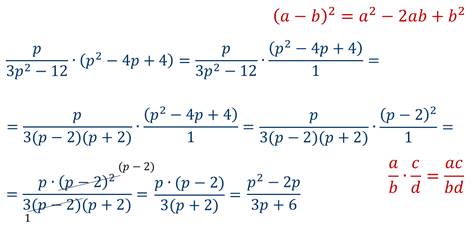
Теперь рассмотрим, как выполняется возведение рациональной дроби в степень.

Проверим это равенство на конкретных примерах.

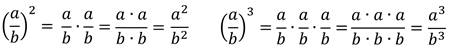
Правило возведения рациональной дроби в степень:

Чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе, а второй в знаменателе дроби.

Пример 5: возвести в третью степень дробь.

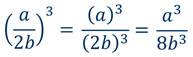
Пример 6: возвести во вторую степень дробь.

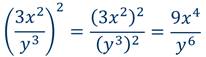
Пример 7:

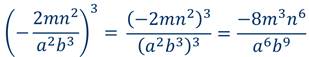
Итоги

Чтобы возвести дробь в степень, надо возвести в эту степеньчислитель и знаменатель и первый результат записать в числителе, а второй в знаменателе дроби.

Если остались вопросы посмотреть видео урок по ссылке https://resh.edu.ru/subject/lesson/1968/main/

Или продолжить изучение темы , работая с учебником

« Алгебра 8 класс» п. 5

Решить: № 110(а,б); 111(а,б); 116(а,б);

Д/З Выучить п. 5 Решить №122

Выполни тренировочные задания по ссылке

https://resh.edu.ru/subject/lesson/1968/train/#154844

ВНИМАНИЕ!!! Выполненную работу и результат теста фотографируешь (вертикально) и пересылаешь мне в vk https://vk.com/id589665126 15 ноября 2021 года