
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Краткие теоретические сведения
10 Сводка основных формул по теме«Механические колебания).08 ноября.
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
Краткие теоретические сведения
Смещение, скорость и ускорение при гармонических колебаниях определяются уравнениями:
 , (5.1)
, (5.1)
 , (5.2)
, (5.2)
 , (5.3)
, (5.3)
где 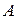 – амплитуда колебания,
– амплитуда колебания, 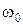 – циклическая частота,
– циклическая частота, 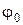 – начальная фаза. Фазой называется величина, стоящая под знаком синуса или косинуса в уравнениях гармонических колебаний.
– начальная фаза. Фазой называется величина, стоящая под знаком синуса или косинуса в уравнениях гармонических колебаний.
Циклическая частота 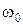 , период
, период 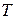 и частота
и частота 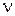 связаны соотношениями:
связаны соотношениями:
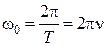 . (5.4)
. (5.4)
Свободные незатухающие гармонические колебания происходят при действии квазиупругой силы без сопротивления и описываются уравнением
 .
.
Сила, действующая на тело при свободных гармонических колебаниях (квазиупругая сила), всегда пропорциональна смещению и направлена в сторону, противоположную смещению:
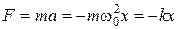 , (5.5)
, (5.5)
где 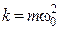 – коэффициент квазиупругости силы, который равен силе F при единичном смещении тела из положения равновесия.
– коэффициент квазиупругости силы, который равен силе F при единичном смещении тела из положения равновесия.
Когда сопротивление среды отсутствует, циклическая частота 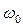 свободных гармонических колебаний, называемая собственной циклической частотой, и период
свободных гармонических колебаний, называемая собственной циклической частотой, и период 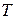 равны:
равны:
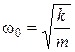 ,
, 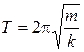 . (5.6)
. (5.6)
Период колебаний математического маятника длины 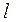 равен
равен
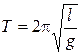 . (5.7)
. (5.7)
Полная энергия тела, которое совершает гармонические колебания, постоянна и равна:
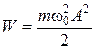 . (5.8)
. (5.8)
Если при колебаниях действует сила сопротивления, пропорциональная скорости ( 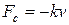 ), то они будут затухающими и описываются уравнением
), то они будут затухающими и описываются уравнением
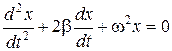 ,
,
где 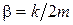 - коэффициент затухания.
- коэффициент затухания.
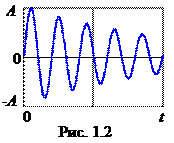
Общее решение уравнения для затухающих колебаний и имеет вид
 ,
,
график этой функции изображен на рис. 1.2.
Под действием внешней периодической силы  точка будет совершать вынужденные колебания по закону
точка будет совершать вынужденные колебания по закону
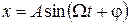
с амплитудой А и фазой j, которые определяются по формулам
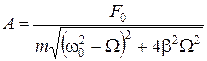 ,
, 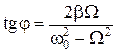 .
.
Если частота вынуждающей силы совпадает с частотой собственных колебаний, то наступает резонанс – резкое возрастание амплитуды колебаний.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|