Примеры решения задач на колебания

10 Примеры решения задач на колебания

Задача 5.1.Материальная точка совершает колебания, при которых ее координата х изменяется со временем t по закону

, (1)

где все величины выражены в единицах СИ. Найти амплитуду, циклическую частоту, частоту, период и начальную фазу колебаний. Вычислить смещение точки при фазе π/3 рад и максимальное значение скорости колеблющейся точки.

Решение. Запишем уравнение движения в общем виде:

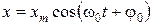. (2)

Сопоставляя уравнения (1) и (2), находим: амплитуда х_m = 0,060 м, циклическая частота ω₀ = 50π рад/с, начальная фаза φ₀ = 0. Теперь найдем частоту ν и период Т колебаний:

, .

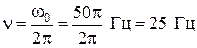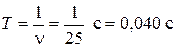При фазе 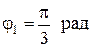смещение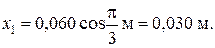

Взяв производную координаты (2) по времени, получим выражение для скорости:

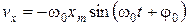Максимальное (амплитудное) значение скорости 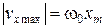. Вычислим:

33. Материальная точка массой m = 50 г совершает гармонические колебания. Амплитуда колебаний А = 5 см, период Т = 4 с. Записать уравнение колебаний точки, приняв за начальное положение 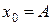. Найти максимальную скорость 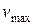колеблющейся точки, максимальное ускорение 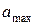и полную механическую энергию точки. Определить координату, скорость и ускорение точки время .

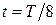Решение. Движение точки с соответствующими начальными условиями описывается гармоническим законом в виде

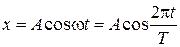, (1)

где 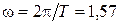с^–1 – циклическая частота.

Скорость точки равна производной от координаты по времени

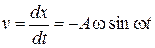. (2)

Скорость, как и координата, изменяется по гармоническому закону. Максимальное значение скорости наблюдается при 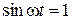и равно

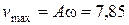см/с.

Ускорение точки равно производной от скорости по времени

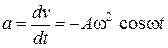Ускорение изменяется по такому же закону, как и координата. Максимальное значение ускорения найдем по формуле

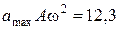см/с².

При колебаниях точки сохраняется полная механическая энергия Е, равная сумме кинетической 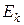и потенциальной 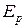энергий: 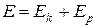. Когда потенциальная энергия равна нулю, кинетическая энергия максимальная и равна полной энергии

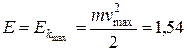Дж.

Значения координаты, скорости и ускорения в момент времени 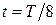найдем по формулам

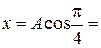3,54 см, 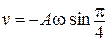= –5,55 см/с, 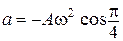= –8,72 см/с².

Задача 5.2.Материальная точка совершает гармонические колебания вдоль оси 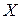. Через время 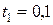с от начала движения смещение точки от положения равновесия 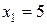см, скорость 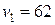см/с, ускорение 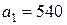см/с². Определить: а) амплитуду, циклическую частоту и начальную фазу колебаний; б) смещение, скорость и ускорение в начальный момент времени.

Решение. Закон движения материальной точки имеет вид:

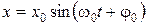Согласно формулам (5.2) и (5.3) скорость и ускорение можно записать как:

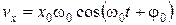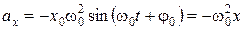Для момента времени 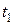имеем:

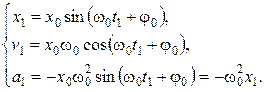
Знак “–” в последнем уравнении указывает на то, что ускорение и смещение противоположны по направлению. Из последнего уравнения можно найти циклическую частоту (определять следует по модулю).

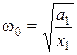Возведем в квадрат первые два уравнения и, сложив их, получим:

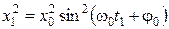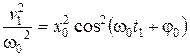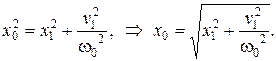
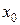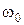Используя условия задачи и найденные величины и , определим начальную фазу колебаний:

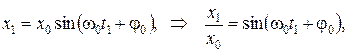
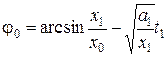Для нахождения значени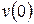й , и 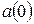– координаты, скорости и ускорения в момент времени 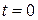, подставим значения 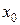и 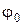в общие уравнения:

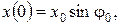
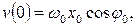
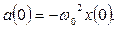
В численных значениях имеем: 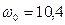рад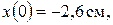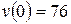/с, см/с, 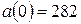см/с², 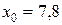см, .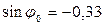

Задача 5.4.Частица массой 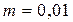кг совершает гармонические колебания с периодом 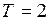с. Общая энергия частицы 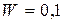мДж. Определить амплитуду колебаний и максимальное значение силы, которая действует на частицу.

Решение. Для определения амплитуды колебаний воспользуемся уравнением для полной энергии частицы

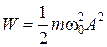Подставив вместо 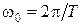, для амплитуды получим:

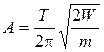Поскольку частица совершает гармонические колебания, то сила, которая действует на нее, является квазиупругой, то есть можем записать, что 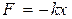, где 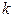– коэффициент упругости (коэффициент квазиупругой силы), 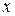– смещение. Максимальное значение сила будет иметь при максимальном смещении, которое, в свою очередь, равно амплитуде. Таким образом,

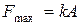Коэффициент 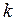найдем с помощью формулы его связи с частотой и периодом

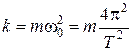Таким образом,

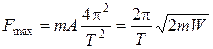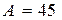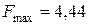Подставив численные значения, получим: мм, мН.

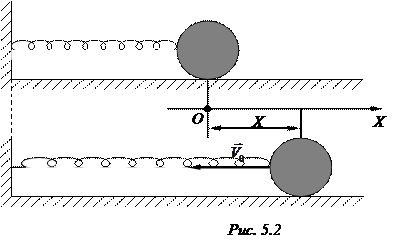
Задача 5.5.На горизонтальной поверхности лежит шарик массой m, прикрепленный к стенке с помощью пружины, жесткость которой равна k. Шарик сместили из положения равновесия на расстояние x₀ и толкнули влево, сообщив ему начальную скорость v₀ (рис. 5.2). Найти амплитуду колебаний. Массой пружины и трением пренебречь.

Решение. Рассмотрим два состояния системы: первое, когда пружина была растянута на величину 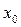и шарику сообщили скорость v₀, и второе, когда шарик максимально сместился влево, пружина сжата. В первом состоянии полная энергия системы складывается из потенциальной энергии растянутой пружины и кинетической энергии шарика:

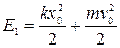Во втором состоянии полная энергия системы равна потенциальной энергии сжатой пружины:

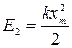где х_m – амплитуда колебаний.

Согласно закону сохранения энергии, Е₁ = Е₂ , или

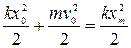Отсюда найдем

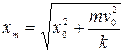Из полученной формулы следует частный случай: при v₀ = 0 имеем х_m = = x₀, т.е. если бы шарик отпустили без начальной скорости, то амплитуда колебаний была бы равна x₀.