
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Алгоритм решения задач на колебания
10 Алгоритм решения задач на колебания
Уравнение гармонических колебаний можно записать двумя способами, основанными на простой связи между синусом и косинусом:
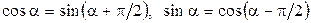 .
.
Поэтому смещение, скорость и ускорение одного и того же гармонического колебания, которое описывается формулами (5.1) – (5.3), всегда можно записать в виде уравнений:
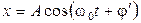 ,
,
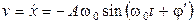 ,
,
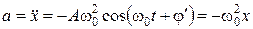 ,
,
где 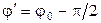 . Начальные фазы
. Начальные фазы 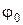 или
или 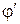 при решении задачи находят из начальных условий: смещения и скорости тела в начальный момент времени.
при решении задачи находят из начальных условий: смещения и скорости тела в начальный момент времени.
Из системы (5.1) – (5.3) следует, что максимальному смещению при гармоническом колебании соответствуют нулевая скорость и максимальное ускорение, направленное противоположно смещению (в сторону равновесия). Наоборот, в положении равновесия 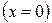 скорость максимальна, а ускорение равно нулю.
скорость максимальна, а ускорение равно нулю.
Алгоритм решения задач на колебания
Уравнение гармонических колебаний можно записать двумя способами, основанными на простой связи между синусом и косинусом:
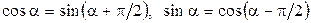 .
.
Поэтому смещение, скорость и ускорение одного и того же гармонического колебания, которое описывается формулами (5.1) – (5.3), всегда можно записать в виде уравнений:
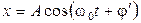 ,
,
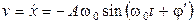 ,
,
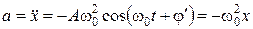 ,
,
где 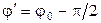 . Начальные фазы
. Начальные фазы 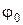 или
или 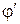 при решении задачи находят из начальных условий: смещения и скорости тела в начальный момент времени.
при решении задачи находят из начальных условий: смещения и скорости тела в начальный момент времени.
Из системы (5.1) – (5.3) следует, что максимальному смещению при гармоническом колебании соответствуют нулевая скорость и максимальное ускорение, направленное противоположно смещению (в сторону равновесия). Наоборот, в положении равновесия 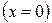 скорость максимальна, а ускорение равно нулю.
скорость максимальна, а ускорение равно нулю.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|