Актуализация опорных знаний. Работа по теме урока

Стр 1 из 2Следующая ⇒

09.11.2021 Алгебра 9 класс

Тема: Квадратный трехчлен и его корни

Цель: Научиться находить корни квадратного трёхчлена .

Ход урока.

Подготовка к уроку. Открыли тетрадь, записали число, Дистанционное обучение

( дальше вся работа по теме урока.т.е. теперь не пишите классная работа, домашняя работа). , тема урока.

1. Актуализация опорных знаний

Устная работа. Чтение графика.

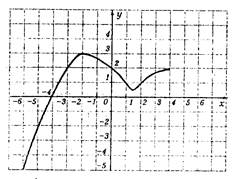
На рисунке изображен график функции f(х). Определите по графику:

l . область определения функции; [-6; 4]

2. область значений функции; [-5; 3]

3. какие значения принимает функция при x = -2; 0; 2; ( у=3; у=2; у=1)

4. какие значения аргумента соответствуют значениям функции, равным 2; 0; -2

(у=2 при х=-3,0,4 у=0 при х=-4 у=-2 при х=-5)

5. какие значения функции принимает только раз; (у=3; [-5; 0,5])

6. при каких значениях аргумента функция положитeльна (f(х) > 0);

( f(х) > 0 при х (-4; 4] )

Работа по теме урока

Изучение нового материала. Записать определения, основные понятия, пример 1 и 2.

Каждое из выражений х⁵-2х⁴+3х³– 7х +2; 2у⁴– у³+5у²-3у +18; 7z⁶-6z⁵+ z²-2z+3 является многочленом с одной переменной.

Значение переменной, при котором многочлен обращается нуль, называют корнем многочлена.

Найдем, например, корни многочлена х³–х. Для этого решим уравнение х³–х=0.

Разложив на множители левую часть уравнения, получим х(х-1)(х+1)=0,

х₁=0, х₂=1, х₃= -1.

Таким образом, числа 0,1,-1 – корни многочлена х³–х.

Многочлен второй степени с одной переменной называют квадратным трехчленом.

Определение. Квадратным трехчленом называют многочлен вида ах²+ вх + с, где х – переменная, а,в,с – некоторые числа, причем а не равно нулю.

Приведем примеры квадратных трехчленов: многочлены

3х²– 5х -2; 25х²–х; 36х².

Для того чтобы найти корни квадратного трехчлена ах²+ вх + с, надо решить квадратное уравнение ах²+ вх + с=0.

Пример 1. Найдите корни квадратного трехчлена 3х²– 2х -5.

Решение: Решим уравнение 3х²– 2х -5=0.

D= 64; х₁=1 ²/_3;х₂= -1.

Значит, квадратный трехчлен 3х²– 2х -5 имеет два корня: 1 ²/₃ и -1.

Так как квадратный трехчлен ах²+ вх + с имеет те же корни, что и квадратное уравнение ах²+ вх + с=0,то он может, как и квадратное уравнение, иметь два корня, один корень или не иметь корней. Это зависит от дискриминанта квадратного уравнения D= b² – 4ac, который называют также дискриминантом квадратного трехчлена. Если D>0, то квадратный трехчлен имеет два корня; если D=0 , то квадратный трехчлен имеет один корень; если D<0, квадратный трехчлен не имеет корней.

При решении задач иногда бывает удобно представить квадратный трехчлен ах²+ вх + с

в виде a(x-m)²+n , где m и n – некоторые числа. Такое преобразование называется выделением квадрата двучлена из квадратного трехчлена. ( Формула сокращенного умножения)

* А теперь давайте вспомним порядок выделение квадрата двучлена. Что нам в этом поможет? (формулы сокращенного умножения)

(а ± в)²= а²±2ав+в²

На что нужно обратить внимание, прежде чем начать выделение квадрата двучлена? (на старший коэффициент а)

Пример 2. Выделить из трехчлена 2х²-24х+84 квадрат двучлена.

Решение: 2х²-24х+84=2(х²-12х+42)=2(х²-2 ^.6 ^.х+36-36+42)=2((х-6)²+6)=2(х-6)²+12.

Значит, 2х²-24х+84=2(х-6)²+12.

12 Следующая ⇒