
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ноября 2021 г. (понедельник)
01 ноября 2021 г. (понедельник)
Дисциплина: Математика: алгебра и начала математического анализа, геометрия.
Группа: № 80
Урок № 44
Тема: Уравнения sin 𝑥 = a.
Учебная: рассмотреть решения тригонометрического уравнения sin 𝑥 = a.
Развивающая: развивать математическое мышление, вычислительные навыки. Воспитательная: воспитывать у обучающихся устойчивый интерес к изучению математики; математическую культуру.
Материалы урока:
Литература: Алгебра и начала математического анализа. 10-11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни / Ш.А. Алимов, Ю.М. Колягин [и др.] – М.: Просвещение, 2012.
Изучить теоретический материал стр. 173-177.
ПИШЕМ В КОНСПЕКТАХ:
Арксинусом числа аÎ[–1; 1] называется такое число a Î 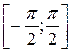 , синус которого равен а: arcsin а = a, если sin a = а и
, синус которого равен а: arcsin а = a, если sin a = а и 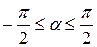 .
.
arcsin (– а) = – arcsin а
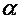
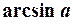
| 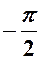
| 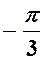
| 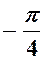
| 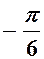
| 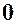
| 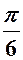
| 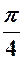
| 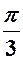
| 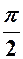
|
| a | 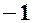
| 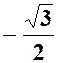
| 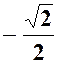
| 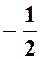
| 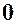
| 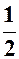
| 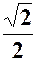
| 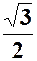
| 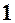
|
Вычислите:
1) arcsin 0 = 0;
2) arcsin 1 = 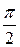 ;
;
3) arcsin 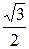 =
= 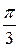 ;
;
4) arcsin 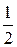 =
= 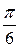 ;
;
5) arcsin 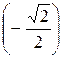 = – arcsin
= – arcsin 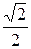 = –
= – 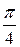 ;
;
6) arcsin 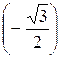 = – arcsin
= – arcsin 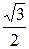 = –
= – 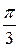 ;
;
7) arcsin 1 – arcsin (– 1) = arcsin 1 + arcsin 1 = 2 arcsin 1 = 2 × 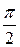 = p ;
= p ;
8) arcsin 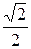 + arcsin
+ arcsin 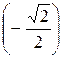 = arcsin
= arcsin 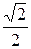 – arcsin
– arcsin 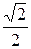 = 0;
= 0;
9) arcsin 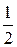 + arcsin
+ arcsin 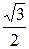 =
= 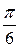 +
+ 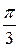 =
= 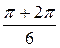 =
= 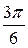 =
= 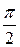 ;
;
10) arcsin 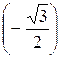 + arcsin
+ arcsin 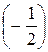 = – arcsin
= – arcsin 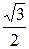 – arcsin
– arcsin 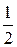 = –
= – 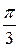 –
– 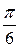 =
= 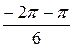 =
=
= – 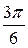 = –
= – 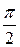 .
.
sin х = а Þ x = (– 1)n arcsin а + πn, n Î Z
sin х = 0 Þ x = πn, n Î Z
sin х = 1 Þ x = 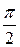 + 2πn, n Î Z
+ 2πn, n Î Z
sin х = – 1 Þ x = – 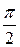 + 2πn, n Î Z
+ 2πn, n Î Z
Решить уравнения:
1) sin x = 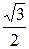
x = (– 1)n arcsin 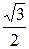 + πn, n Î Z
+ πn, n Î Z
x = (– 1)n 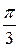 + πn, n Î Z
+ πn, n Î Z
Ответ: (– 1)n 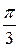 + πn, n Î Z.
+ πn, n Î Z.
2) sin x = 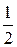
x = (– 1)n arcsin 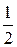 + πn, n Î Z
+ πn, n Î Z
x = (– 1)n 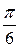 + πn, n Î Z
+ πn, n Î Z
Ответ: (– 1)n 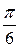 + πn, n Î Z.
+ πn, n Î Z.
Домашнее задание: выполнить № 589 (2,3) стр.178.
ФОТОГРАФИРУЕМ И ОТСЫЛАЕМ ЕЛЕНЕ АНАТОЛЬЕВНЕ
ВСЕ ВЫПОЛНЕННЫЕ ДОМАШНИЕ ЗАДАНИЯ И КОНТРОЛЬНЫЕ РАБОТЫ!!!!!!!
Урок № 45
Тема: Уравнения tgx = a.
Учебная: рассмотреть решение простейшего тригонометрического уравнения tgx = a.
Развивающая: развивать математическое мышление, вычислительные навыки.
Воспитательная: воспитывать у обучающихся устойчивый интерес к изучению математики; математическую культуру.
Материалы урока:
Литература: Алгебра и начала математического анализа. 10-11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни / Ш.А. Алимов, Ю.М. Колягин [и др.] – М.: Просвещение, 2012.
Изучить теоретический материал стр. 179-183.
ПИШЕМ В КОНСПЕКТАХ:
Арктангенсом числа аÎ R называется такое число a Î 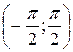 , тангенс которого равен а: arctg а = a, если tg a = а и –
, тангенс которого равен а: arctg а = a, если tg a = а и – 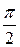 < a <
< a < 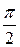 .
.
arctg (– а) = – arctg а
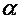
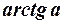
| 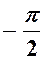
| 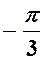
| 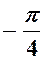
| 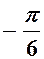
| 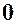
| 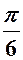
| 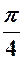
| 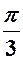
| 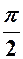
|
| a | - | 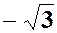
| 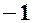
| 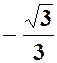
| 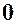
| 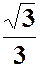
| 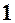
| 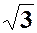
| - |
Вычислите:
1) arctg 0 = 0;
2) arctg (– 1) = – arctg 1 = – 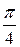 ;
;
3) arctg 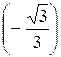 = – arctg
= – arctg 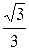 = –
= – 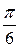 ;
;
4) arctg 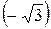 = – arctg
= – arctg 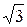 = –
= – 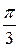 ;
;
5) 6 arctg 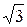 – 4 arcsin
– 4 arcsin 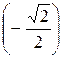 = 6 arctg
= 6 arctg 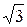 + 4 arcsin
+ 4 arcsin 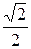 = 6 ×
= 6 × 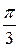 + 4 ×
+ 4 × 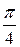 = 2p + p =
= 2p + p =
= 3p ;
6) 2 arctg 1 + 3 arcsin 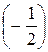 = 2 arctg 1 – 3 arcsin
= 2 arctg 1 – 3 arcsin 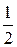 = 2 ×
= 2 × 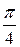 – 3 ×
– 3 × 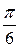 =
= 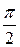 –
– 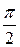 = 0;
= 0;
7) 5 arctg 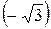 – 3 arcсоs
– 3 arcсоs 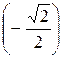 = – 5 arctg
= – 5 arctg 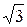 – 3
– 3 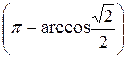 = – 5 ×
= – 5 × 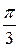 –
–
– 3 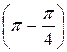 = –
= – 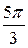 – 3 ×
– 3 × 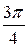 = –
= – 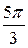 –
– 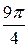 =
= 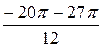 =
= 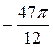 .
.
Решить уравнения:
1) tg x = 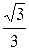
x = arctg 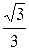 + πn, n Î Z
+ πn, n Î Z
x = 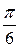 + πn, n Î Z
+ πn, n Î Z
Ответ: 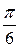 + πn, n Î Z.
+ πn, n Î Z.
2) tg x = – 1
x = arctg (– 1) + πn, n Î Z
x = – 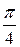 + πn, n Î Z
+ πn, n Î Z
Ответ: – 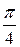 + πn, n Î Z.
+ πn, n Î Z.
3) tg x = 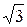
x = arctg 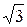 + πn, n Î Z
+ πn, n Î Z
x = 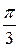 + πn, n Î Z
+ πn, n Î Z
Ответ: 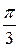 + πn, n Î Z.
+ πn, n Î Z.
Домашнее задание: прислать конспект урока.
ФОТОГРАФИРУЕМ И ОТСЫЛАЕМ ЕЛЕНЕ АНАТОЛЬЕВНЕ
ВСЕ ВЫПОЛНЕННЫЕ ДОМАШНИЕ ЗАДАНИЯ И КОНТРОЛЬНЫЕ РАБОТЫ!!!!!!!
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|