| II.
| Основная часть. Теоретическая часть.
Прямая, точка, луч, отрезок и угол– это то, с чего вы начали изучать геометрию.
Сегодня вспомним, что вы узнали из первых уроков геометрии; закрепим навыки построения изученных геометрических фигур; вспомним, как решать задачи на измерения и вычисления.
Для начала, вспомним, что такое геометрия. Геометрия одна из древнейших наук, она возникла из потребностей человека, связанных с различного рода измерительными работами, как на земельных участках, так и при строительстве зданий. Носегодня геометрия – это наука, занимающаяся изучением геометрических фигури отношений между ними.
Вспомним, некоторые понятия из геометрии. Поговорим о точках, прямых, отрезках, для начала вспомним, как они обозначаются.
Две пересекающиеся прямые называются перпендикулярными (или взаимно перпендикулярными), если они образуют при пересечениичетыре прямых угла.
Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными.
Геометрия – это наука, занимающаяся изучением геометрических фигур.
Часть прямой, ограниченную точками, называют отрезком.
Точки, ограничивающие отрезок, называются концами отрезка.
Луч – часть прямой, состоящей из всех точек, лежащих по одну сторону от заданной точкии сама точка, которая является началом луча.
Два угла называются вертикальными, если стороны одного угла являются продолжением сторон другого угла. Такие углы равны.
 ∠АОВ и ∠ВОС – смежные.
∠АОВ и ∠ВОС – смежные.
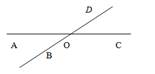 ∠АОВ + ∠ВОС =180°.
∠АОВ и ∠DОС – вертикальные.
∠АОВ = ∠DОС.
Докажем следующее утверждение: если биссектрисы углов ВМР и ВМК перпендикулярны, то точки К, М, Р лежат на одной прямой.
Доказательство.
Сделаем рисунок к заданию. ∠АОВ + ∠ВОС =180°.
∠АОВ и ∠DОС – вертикальные.
∠АОВ = ∠DОС.
Докажем следующее утверждение: если биссектрисы углов ВМР и ВМК перпендикулярны, то точки К, М, Р лежат на одной прямой.
Доказательство.
Сделаем рисунок к заданию.  По условию ∠ОМТ = 90° (т.к. МО ┴ МТ).
∠ОМТ = ∠ОМВ +∠ВМТ.
∠КМР =∠ ВМК +∠ ВМР = (∠ КМО +∠ОМВ) +(∠ВМТ +∠ ТМР).
∠ КМО = ∠ОМВ и ∠ВМТ = ∠ТМР (по определению биссектрисы, т.к. по условию, МО и МТ – биссектрисы углов ВМР и ВМК).
∠КМР = 2 · ∠ОМВ + 2 ·∠ВМТ = 2(∠ОМВ +∠ВМТ) = 2· 90° =180°, следовательно, угол КМР развёрнутый (по свойству развернутого угла).
По определению развёрнутого угла его обе стороны КМ и МР лежат на одной прямой. Следовательно, точки К, М, Р лежат на одной прямой.
Что и требовалось доказать.
По условию ∠ОМТ = 90° (т.к. МО ┴ МТ).
∠ОМТ = ∠ОМВ +∠ВМТ.
∠КМР =∠ ВМК +∠ ВМР = (∠ КМО +∠ОМВ) +(∠ВМТ +∠ ТМР).
∠ КМО = ∠ОМВ и ∠ВМТ = ∠ТМР (по определению биссектрисы, т.к. по условию, МО и МТ – биссектрисы углов ВМР и ВМК).
∠КМР = 2 · ∠ОМВ + 2 ·∠ВМТ = 2(∠ОМВ +∠ВМТ) = 2· 90° =180°, следовательно, угол КМР развёрнутый (по свойству развернутого угла).
По определению развёрнутого угла его обе стороны КМ и МР лежат на одной прямой. Следовательно, точки К, М, Р лежат на одной прямой.
Что и требовалось доказать.
| Работа учащихся с учебником.
Самостоятельная работа.
| 30 мин.
| Рассказ учителя, самостоятельная работа учащихся
|
| III.
| Закрепление изученного материала.
Запишем в тетрадь 1. На рисунке прямые СМ и АD пересекаются в точке О. Найдите градусную меру углов МОС, АОМ, МОD.
Решение.
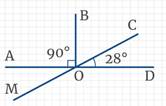 ∠АОМ =∠СОD = 28°(как вертикальные углы).
∠МОD и ∠СОD – смежные, следовательно, ∠МОD + ∠СОD =180°.
Поэтому ∠МОD 180° – ∠СОD =180° – 28° = 152°.
∠МОС – развёрнутый, следовательно, равен 180°.
Ответ: ∠МОС =180°;∠МОD =152°; ∠АОМ=28°.
Работа с учебником
Ответить на вопросы стр.25-26 №15,18-20 (Устно)
∠АОМ =∠СОD = 28°(как вертикальные углы).
∠МОD и ∠СОD – смежные, следовательно, ∠МОD + ∠СОD =180°.
Поэтому ∠МОD 180° – ∠СОD =180° – 28° = 152°.
∠МОС – развёрнутый, следовательно, равен 180°.
Ответ: ∠МОС =180°;∠МОD =152°; ∠АОМ=28°.
Работа с учебником
Ответить на вопросы стр.25-26 №15,18-20 (Устно)
| Работа учащихся с заданиями стр.25-26
| 7 мин.
| Самостоятельная работа
|

 ∠АОВ и ∠ВОС – смежные.
∠АОВ и ∠ВОС – смежные.
 ∠АОВ + ∠ВОС =180°.
∠АОВ и ∠DОС – вертикальные.
∠АОВ = ∠DОС.
Докажем следующее утверждение: если биссектрисы углов ВМР и ВМК перпендикулярны, то точки К, М, Р лежат на одной прямой.
Доказательство.
Сделаем рисунок к заданию.
∠АОВ + ∠ВОС =180°.
∠АОВ и ∠DОС – вертикальные.
∠АОВ = ∠DОС.
Докажем следующее утверждение: если биссектрисы углов ВМР и ВМК перпендикулярны, то точки К, М, Р лежат на одной прямой.
Доказательство.
Сделаем рисунок к заданию.  По условию ∠ОМТ = 90° (т.к. МО ┴ МТ).
∠ОМТ = ∠ОМВ +∠ВМТ.
∠КМР =∠ ВМК +∠ ВМР = (∠ КМО +∠ОМВ) +(∠ВМТ +∠ ТМР).
∠ КМО = ∠ОМВ и ∠ВМТ = ∠ТМР (по определению биссектрисы, т.к. по условию, МО и МТ – биссектрисы углов ВМР и ВМК).
∠КМР = 2 · ∠ОМВ + 2 ·∠ВМТ = 2(∠ОМВ +∠ВМТ) = 2· 90° =180°, следовательно, угол КМР развёрнутый (по свойству развернутого угла).
По определению развёрнутого угла его обе стороны КМ и МР лежат на одной прямой. Следовательно, точки К, М, Р лежат на одной прямой.
Что и требовалось доказать.
По условию ∠ОМТ = 90° (т.к. МО ┴ МТ).
∠ОМТ = ∠ОМВ +∠ВМТ.
∠КМР =∠ ВМК +∠ ВМР = (∠ КМО +∠ОМВ) +(∠ВМТ +∠ ТМР).
∠ КМО = ∠ОМВ и ∠ВМТ = ∠ТМР (по определению биссектрисы, т.к. по условию, МО и МТ – биссектрисы углов ВМР и ВМК).
∠КМР = 2 · ∠ОМВ + 2 ·∠ВМТ = 2(∠ОМВ +∠ВМТ) = 2· 90° =180°, следовательно, угол КМР развёрнутый (по свойству развернутого угла).
По определению развёрнутого угла его обе стороны КМ и МР лежат на одной прямой. Следовательно, точки К, М, Р лежат на одной прямой.
Что и требовалось доказать.
 ∠АОМ =∠СОD = 28°(как вертикальные углы).
∠МОD и ∠СОD – смежные, следовательно, ∠МОD + ∠СОD =180°.
Поэтому ∠МОD 180° – ∠СОD =180° – 28° = 152°.
∠МОС – развёрнутый, следовательно, равен 180°.
Ответ: ∠МОС =180°;∠МОD =152°; ∠АОМ=28°.
Работа с учебником
Ответить на вопросы стр.25-26 №15,18-20 (Устно)
∠АОМ =∠СОD = 28°(как вертикальные углы).
∠МОD и ∠СОD – смежные, следовательно, ∠МОD + ∠СОD =180°.
Поэтому ∠МОD 180° – ∠СОD =180° – 28° = 152°.
∠МОС – развёрнутый, следовательно, равен 180°.
Ответ: ∠МОС =180°;∠МОD =152°; ∠АОМ=28°.
Работа с учебником
Ответить на вопросы стр.25-26 №15,18-20 (Устно)