Лекционный материал. Задачи на размещения. Типичная смысловая нагрузка: «Сколькими способами можно выбрать k объектов и в каждой выборке переставить их местами?»

Лекционный материал

Задачи на размещения

Имеется 5 книг и одна полка, такая что на ней вмещается лишь 3 книги.

Сколькими способами можно расставить на полке 3 книги?

Это задача на размещение.

Решение:Выбираем одну из 5-ти книг и ставим на первое место на полке. Это можно сделать 5-ю способами.

Вторую книгу мы можем выбрать 4-мя способами и поставить рядом с одной из 5-ти возможных первых.

Таких пар может быть 5·4.

Третью книгу мы можем выбрать 3-мя способами.

Получится 5·4·3 разнообразных троек. Значит всего способов разместить 3 книги из 5-ти 5·4·3 = 60.

Ответ:60.

Определение:Размещением из n элементов по k (k≤n) называется любое множество, состоящее из k элементов, взятых в определённом порядке из данных n элементов.

Формула: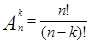

Типичная смысловая нагрузка: «Сколькими способами можно выбрать k объектов и в каждой выборке переставить их местами?»

Пример 1.Учащиеся второго класса изучают 9 предметов. Сколькими способами можно составить расписание на один день, чтобы в нём было 4 различных предмета?

Решение: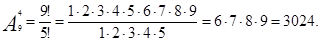

Ответ:3024.

Пример 2.Сколько трехзначных чисел можно составить из цифр 2, 4, 6, 7, 9?

Решение: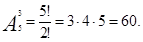

Ответ:60.

Пример 3.В соревнованиях высшей лиги по футболу участвуют 18 команд. Борьба идет за золотые, серебряные и бронзовые медали. Сколькими способами могут быть распределены медали между командами?

Решение: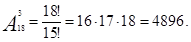

Ответ:4896.

Пример 4.Сколькими способами можно опустить 5 писем в 11 почтовых ящиков, если в каждый ящик опускают не более одного письма?

Решение: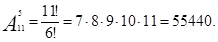

Ответ:55440.

Пример 5.Боря, Дима и Володя сели играть в карты. Сколькими способами им можно сдать по одной карте? (колода содержит 36 карт)

Решение:

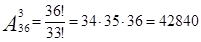– способами можно раздать 3 карты игрокам.

Ответ:42840.

Пример 6.В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человека, при условии, что все они должны ехать в различных вагонах?

Решение:

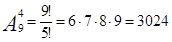– способами можно рассадить в поезде 4 человека.

Ответ:3024.

Практическая часть

Решаете все номера