
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Метод Крамера. Метод Гаусса







Метод Крамера




Матричный метод 






Метод Гаусса
Метод Гаусса, называемый также методом последовательного исключения неизвестных, состоит в следующем. При помощи элементарных преобразований систему линейных уравнений приводят к такому виду, чтобы её матрица из коэффициентов оказалась трапециевидной (то же самое, что треугольной или ступенчатой) (прямой ход метода Гаусса).
После того, как матрица системы приняла трапециевидную форму, уже не представляет труда разобраться в вопросе о совместности системы, определить число решений и найти сами решения.
В такой системе, называемой трапециевидной, последнее уравнение содержит только одну переменную и её значение можно однозначно найти. Затем значение этой переменной подставляют в предыдущее уравнение (обратный ход метода Гаусса), из которого находят предыдущую переменную, и так далее.
При решении систем линейных уравнений с любым числом уравнений и неизвестных в системе уравнений и в расширенной матрице системы можно:
1. переставлять местами строки (столбцы);
2. если в результате других преобразований появились равные или пропорциональные строки, их можно удалить, кроме одной;
3. удалять "нулевые" строки, где все коэффициенты равны нулю;
4. любую строку умножать или делить на некоторое число;
5. к любой строке прибавлять другую строку, умноженное на некоторое число.
В результате элементарных преобразований получаем систему линейных уравнений, эквивалентную данной.
Пример . Решить методом Гаусса систему линейных уравнений
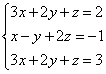
Для упрощения внешнего вида решения составим расширенную матрицу системы:
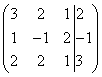
В этой матрице слева до вертикальной черты расположены коэффициенты при неизвестных, а справа после вертикальной черты - свободные члены.
Для удобства деления коэффициентов при переменных (чтобы получить деление на единицу) переставим местами первую и вторую строки матрицы системы. Получим систему, эквивалентную данной, так как в системе линейных уравнений можно переставлять местами уравнения:
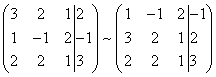
С помощью нового первого уравнения исключим переменную x из второго и всех последующих уравнений. Для этого ко второй строке матрицы прибавим первую строку, умноженную на 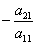 (в нашем случае на -3), к третьей строке – первую строку, умноженную на
(в нашем случае на -3), к третьей строке – первую строку, умноженную на 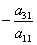 (в нашем случае на -2).
(в нашем случае на -2).
Это возможно, так как 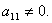
Если бы в нашей системе уравнений было больше трёх, то следовало бы прибавлять и ко всем последующим уравнениям первую строку, умноженную на отношение соответствующих коэффициентов, взятых со знаком минус.
В результате получим матрицу эквивалентную данной системе новой системы уравнений, в которой все уравнения, начиная со второго не содержат переменнную x:
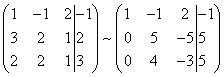
Для упрощения второй строки полученной системы умножим её на 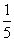 и получим вновь матрицу системы уравнений, эквивалентной данной системе:
и получим вновь матрицу системы уравнений, эквивалентной данной системе:
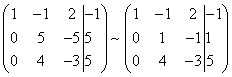
Теперь, сохраняя первое уравнение полученной системы без изменений, с помощью второго уравнения исключаем переменную y из всех последующих уравнений. Для этого к третьей строке матрицы системы прибавим вторую строку, умноженную на 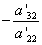 (в нашем случае на -4).
(в нашем случае на -4).
Если бы в нашей системе уравнений было больше трёх, то следовало бы прибавлять и ко всем последующим уравнениям вторую строку, умноженную на отношение соответствующих коэффициентов, взятых со знаком минус.
В результате вновь получим матрицу системы, эквивалентной данной системе линейных уравнений:
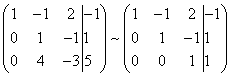
Мы получили эквивалентную данной трапециевидную систему линейных уравнений:
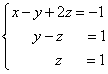
Решение найдём "с конца" - обратный ход. Для этого из последнего уравнения определим z: 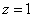 . Подставив это значение в предшествующее уравнение, найдём y:
. Подставив это значение в предшествующее уравнение, найдём y:
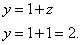 Из первого уравнения найдём x:
Из первого уравнения найдём x: 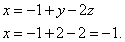
Ответ: решение данной системы уравнений - 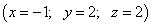 .
.




|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|