Графы. Задания. Домашние задания

Графы

Графом называется геометрическая фигура, состоящая из точек и соединяющих их линий. Точки называются вершинами графа, а линии — ребрами.

Два ребра называются смежными, если они имеют общую вершину.

Два ребра называются кратными, если они соединяют одну и ту же пару вершин. Ребро называется петлей, если его концы совпадают.

Степенью вершины называют количество ребер, для которых она является концевой (при этом петли считают дважды).

Вершина называется изолированной, если она не является концом ни для одного ребра.

Вершина называется висячей, если из неё выходит ровно одно ребро.

Граф без кратных ребер и петель называется обыкновенным.

Лемма о рукопожатиях: В любом графе сумма степеней всех вершин равна удвоенному числу ребер.

Следствие: В любом графе число вершин нечетной степени четно.

Задания

1. Волейбольная сетка имеет вид прямоугольника размером 50×600 клеток. Какое наибольшее число верёвочек можно перерезать так, чтобы сетка не распалась на куски? [1]

2. На кошачьей выставке каждый посетитель погладил ровно трех кошек. При этом оказалось, что каждую кошку погладили ровно три посетителя. Докажите, что посетителей было ровно столько же, сколько кошек. [3]

3. В классе 30 человек. Может ли быть так, что 9 из них имеют по 3 друга (в этом классе), 11 – по 4 друга, а 10 – по 5 друзей? [1]

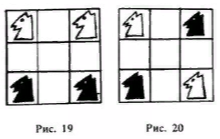
4. Можно ли, сделав несколько ходов конями из исходного положения, изображенного на рис.19, расположить их так, как показано на рис.20? [1]

5. Докажите, что граф с 𝑛 вершинами, степень каждой из которых не менее 𝑛−12 – связан. [2]

6. Между девятью планетами Солнечной системы введено космическое сообщение. Ракеты летают по следующим маршрутам: Земля – Меркурий, Плутон – Венера, Земля – Плутон, Плутон – Меркурий, Меркурий – Венера, Уран – Нептун, Нептун – Сатурн, Сатурн – Юпитер, Юпитер – Марс и Марс – Уран. Можно ли добраться с Земли до Марса? [1]

Домашние задания

1. В классе 30 человек. Может ли быть так, что 9 из них имеют по 3 друга (в этом классе), 11 – по 4 друга, а 10 – по 5 друзей? [1]

2. Из полного 100-вершинного графа выкинули 98 рёбер. Доказать, что он остался связным. [3]

Список источников

1. Генкин, С.А. Ленинградские математические кружки : пособие для внеклассной работы. – Киров.: изд. «АСА», 1994. – 272 с.

2. Спивак, А.В. Тысяча и одна задача по математике: кн. для учащихся 5-7 кл. / А.В. Спивак. – М.: Просвещение, 2002. – 207 с.

3. Электронный ресурс – http://problems.ru/