Практическое занятие № 2. Тема: НАХОЖДЕНИЕ КРИТИЧЕСКОГО ПУТИ В СЕТИ. С ПОМОЩЬЮ АЛГОРИТМА БЕЛЛМАНА–КАЛАБА. Алгоритм Беллмана–Калаба

Практическое занятие № 2

Тема: НАХОЖДЕНИЕ КРИТИЧЕСКОГО ПУТИ В СЕТИ

С ПОМОЩЬЮ АЛГОРИТМА БЕЛЛМАНА–КАЛАБА

Цель работы– на основании алгоритма Беллмана–Калаба научиться находить критический путь в транспортной сети.

Краткие теоретические сведения.

Задача о критическом пути формулируется следующим образом. Задаётся орграф, который называется транспортной сетью, каждой дуге которого 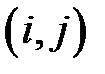соответствует некоторая величина – длина дуги 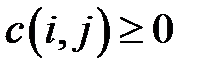. Необходимо найти кратчайший путь из истока 0 в сток z.

Для нахождения критического пути в сети рассмотрим алгоритм Беллмана-Калаба. Он основан на принципе оптимальности и использует функциональное уравнение Беллмана. Принцип оптимальности Беллмана в данном случае можно сформулировать так: любой максимальный (критический) путь, содержащий не более 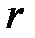дуг, образован частичными путями, содержащими не более 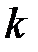дуг, 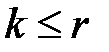, которые (пути) также максимальны.

Алгоритм Беллмана–Калаба

Пусть 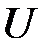– множество дуг, которые образуют сеть, 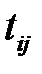– время выполнения операции. Для любой дуги 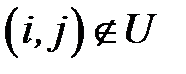полагаем 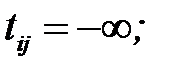с другой стороны, для всякого 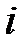полагаем 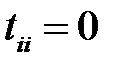. Задача заключается в нахождении пути

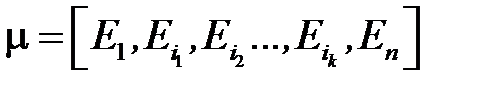(1)

такого, что

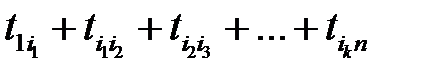(2)

достигает максимума.

Для этого достаточно решить следующую систему уравнений (уравнения Беллмана)

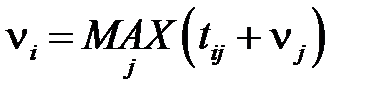
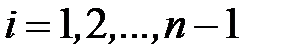(3)

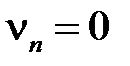(4)

где 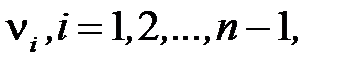представляет собой величину оптимального пути от вершины 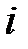до конечной вершины. Все 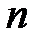вершин считаются пронумерованными от 1 до 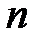(начальная вершина – 1, конечная – ).

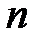Вычисления проводятся следующим способом:

сначала полагаем

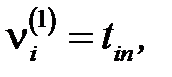
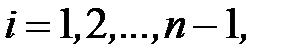(5)

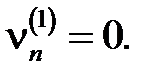(6)

Потом вычисляем

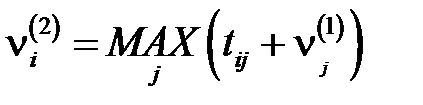
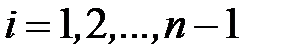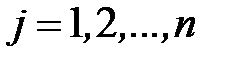, (7)

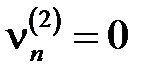(8)

Потом последовательно вычисляем

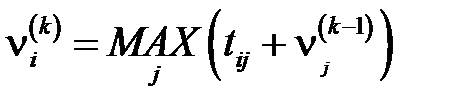
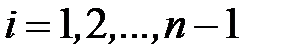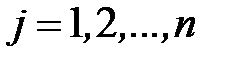, (9)

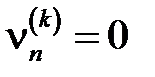(10)

для всех значений 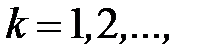вычисления заканчиваются, когда

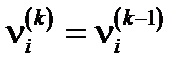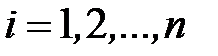, (11)

Тогда 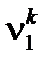будет величиной оптимального пути между вершинам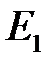и и 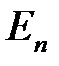. Просто доказывается, что если сеть имеет 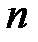вершин, то достаточно 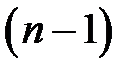итерация для достижения оптимума.

12 Следующая ⇒