
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задание 3. Непосредственное интегрирование.
Задание 2
1)Исследовать функцию и построить её график:
y= 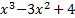
| 2) Исследовать функцию и построить её график:
y= 
|
3) Исследовать функцию и построить её график:
y= 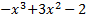
| 4) Исследовать функцию и построить её график:
y= 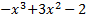
|
5)Исследовать функцию и построить её график:
y= 
| 6) Исследовать функцию и построить её график:
y= 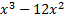 -9x+1 -9x+1
|
7) Исследовать функцию и построить её график:
y= 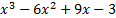
| 8) Исследовать функцию и построить её график:
y= 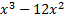 -9x+1 -9x+1
|
9) Исследовать функцию и построить её график:
y= 
| 10) Исследовать функцию и построить её график:
y= 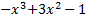
|
Задание 3. Непосредственное интегрирование.
1)  2)
2) 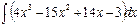 3)
3) 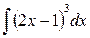
4) 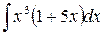 5)
5)  6)
6) 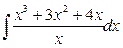
7) 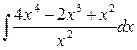 8)
8) 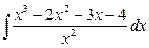 9)
9) 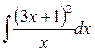
10) 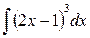
Задание 4.Способ подстановки.
1) 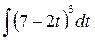 2)
2)  3)
3) 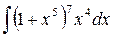
4) 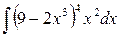 5)
5)  6)
6) 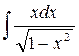
7)  8)
8) 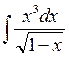 9)
9) 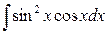
10) 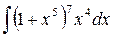
Задания 5. Способ интегрирования по частям.
1) 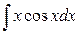 2)
2)  3)
3) 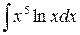
4) 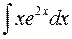 5)
5) 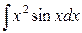 6)
6) 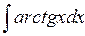
7) 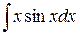 8)
8) 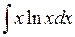 9)
9) 
10) 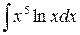
Практическая работа №3. Применение определенного интеграла к решению прикладных задач. Решение задач на вычисление вероятности с использованием элементов комбинаторики.
Цель работы. Отработать навыки применения определенных интегралов при решении прикладных задач. Сформировать умение применять формулы комбинаторики в решении задач на вычисление вероятности.
Приложение
Задание 1.Вычислите определенные интегралы методом непосредственного интегрирования
1) 
| 6) 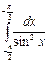
|
2) 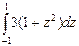
| 7) 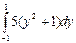
|
3) 
| 8) 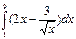
|
4) 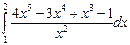
| 9) 
|
5) 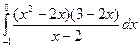
| 10) 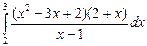
|
Задание 2.Найдите площадь фигуры, ограниченной данными линиями
| № варианта | Уравнения линий |
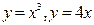
| |

| |

| |
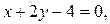 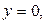 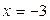 и и 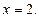
| |
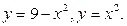
| |
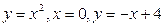
| |
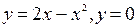
| |
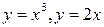
| |
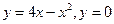
| |
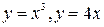
|
Задание 3.Решите задачи с помощью определенного интеграла
1) Найти работу производимую при сжатии пружины на 0,03 м, если для сжатия её на 0,005 м нужно приложить силу в 10 Н.
2) Сила упругости пружины, растянутой на 0,05 м, равна 3 Н. Найти работу, которую надо произвести, чтобы растянуть эту пружину на 0,05 м
3) Найти работу, которую нужно затратить, чтобы растянуть пружину на 0,05 м, если сила 100 Н растягивает пружину на 0,01 м
4) Вычислить работу, совершаемую при сжатии пружины на 15 см, если известно, что для сжатия пружины на 1 см необходима сила в 30 Н.
5) Вычислить работу, совершаемую при сжатии пружины а 0,08 м, если для сжатия её на 0,01 м нужна Сида в 25 Н.
6) Тело движется прямолинейно со скоростью 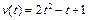 (м/с). Найти путь, пройденный за первые 3 с.
(м/с). Найти путь, пройденный за первые 3 с.
7) Тело движется прямолинейно со скоростью 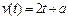 (м/с). найти значение параметра
(м/с). найти значение параметра  , если известно, что за промежуток времени от
, если известно, что за промежуток времени от 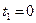 до
до  (с) тело прошло путь длиной 40 м.
(с) тело прошло путь длиной 40 м.
8) Тело движется прямолинейно со скоростью 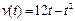 (м/с). Найти длину пути, пройденного телом от начала пути, до его остановки.
(м/с). Найти длину пути, пройденного телом от начала пути, до его остановки.
9) Найти путь, пройденный точкой за третью секунду, зная скорость её прямолинейного движения 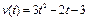 (м/с).
(м/с).
10) Найти работу производимую при сжатии пружины на 0,03 м, если для сжатия её на 0,005 м нужно приложить силу в 10 Н.
Задание 4.
| №1. Из 40 вопросов, входящих в экзаменационные билеты, студент знает 30. Найти вероятность того, что среди трех наугад выбранных вопросов студент знает 2 вопроса. |
| №2. В лотерее разыгрывается 100 билетов. Выигрыши выпали на 20 билетов. Некто приобрел 5 билетов. Найти вероятность того, что выигрыш выпадет хотя бы на один билет. |
| №3.Какова вероятность того, что два определенных студента будут посланы на практику в город С, если в наличии имеется 5 мест в город А, 8- в город В и 7 – в город С. |
| №4. Один студент выучил 20 из 25 вопросов программы по математике, а второй - только 15. каждому из них задают по одному вопросу. Найти вероятность того, что правильно ответит только первый студент. |
| №5. Из букв А, А, И, Л, М, Н разрезной азбуки выбирают наудачу по одной и ставят в ряд. Найти вероятность того, что получится слово: МИНА. |
| №6. В ящике содержаться 9 белых , 6 черных и 5 зеленых шаров. Наудачу вынимается один шар. Найти вероятность того, что он окажется либо черным, либо зеленым. |
| №7. В ящике находится 20 деталей, 4 из них – нестандартные. Какова вероятность того, что среди 6 наугад взятых деталей нестандартных не окажется? |
| №8. В группе 10 юношей и 10 девушек. Для дежурства путем жеребьевки выделяют 5 человек. Какова вероятность того, что в число дежурных войдут 2 юношей и 3 девушки? |
| №9. Три стрелка делают по одному выстрелу в цель. Вероятности попаданий в цель соответственно равны 0,6; 0,85; 0,7. Какова вероятность попадания в цель только второго стрелка? |
| №10.Какова вероятность того, что два определенных студента будут посланы на практику в город С, если в наличии имеется 5 мест в город А, 8- в город В и 7 – в город С. |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|