Напряжения на произвольной площадке при линейном напряженном состоянии.

33. Напряжения на произвольной площадке при линейном напряженном состоянии.

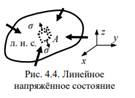
Рассмотрим деталь произвольной формы, нагруженную уравновешенной системой сил (рис. 4.4). Пусть, хотя бы в одной точке А этой детали, реализуется линейное напряжённое состояние.

Рассмотрим брус при центральном растяжении или сжатии (рис. 4.5, а). Покажем, что при центральном растяжении действует лишь одно из главных напряжений. Вырежем в окрестности произвольной точки B элемент, верхняя и нижняя грани которого перпендикулярны оси бруса. На этих гранях действуют только нормальное напряжение, касательных напряжений нет. На боковых гранях, нет ни нормальных, ни касательных напряжений (слои друг на друга не давят), то есть, имеет место линейное напряжённое состояние (рис. 4.5, б).

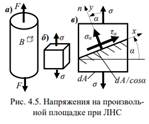
Покажем произвольную площадку, проходящую через данную точку. Положение этой площадки (рис. 4.5, в) определяется нормалью п, то есть углом α (σ ^ σ_α ). Рассмотрим действие верхней части элемента на нижнюю. Введем следующее правило знаков для угла α: при повороте нормали против хода часовой стрелки угол положительный, а при повороте по ходу часовой стрелки – отрицательный. Если обозначить через dA площадь нижней грани элемента, то площадь наклонной площадки будет равна dA/cos α.

Покажем нормальное σ_α и касательное τ_α напряжения, действующие на площадке α, и выразим их через σ. Направим ось у по направлению σ_α , а ось х – по направлению τ_α и составим уравнения равновесия для нижней части элемента

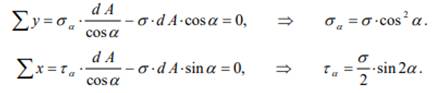
Таким образом, мы получили формулы для определения напряжений на произвольной площадке при линейном напряжённом состоянии.

Проанализируем полученные формулы.

Формула для нормальных напряжений:

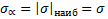при 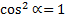или при 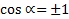; 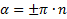, × где n = 0, ±1, ±2, то есть при любых 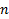попадаем на те же главные площадки. Следовательно, наибольшие нормальные напряжения действуют на главных площадках.

Формула для касательных напряжений даёт:

τ_α = |τ|_наиб = σ/2, при sin2α = ±1; 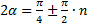где п = 0, ±1, ±2, …

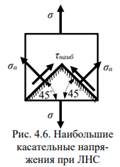
Следовательно, какое бы 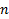не брали, всегда будем попадать на одну из площадок, наклонённых к главным площадкам под углом 45° (рис. 4.6). Строго говоря, |τ| наиб действуют по конической поверхности.